No.10544　事前事後デザインの分析方法について　　【好夫】　2009/07/31(Fri) 15:49

いつもいつもお世話になっています。

トレーニング効果を実験群と統制群を作って事前事後テストで調べたい のですが，事前テストの結果を共変数としてANCOVAで行うのが良いと聞きました。事前・事後3種類のテストがあるのですが，そのうちの一つが「回帰直 線の平行性」という前提をクリアできませんでした。その一つだけをt検定で報告しようと思うのですが，問題でしょうか。
No.10547　Re: 事前事後デザインの分析方法について　　【波音】　2009/07/31(Fri) 20:17

> そのうちの一つが「回帰直線の平行性」という前提をクリアできませんでした。

共分散分析モデル(連続型とカテゴリカル型が混在するモデル)において，当てはめられる数本の回帰直線が平行であるということは連続型の変数とカテゴリカル型の変数の交互作用がないからです(つまり加法モデルが当てはめられたということ)。

こ れに対して，連続型の変数とカテゴリカル型の変数の交互作用が認められる場合には，数本の回帰直線は並行にはなりません。つまり，傾きの違う直線が引かれ るということです(換言すれば，これは連続型の変数の傾きがカテゴリカル型の変数の水準によって変わるということです)。

だから，回帰直線の平行性という前提をクリアできない，ということは交互作用が存在するということです。それで共分散分析が行えないということではないわけです。
No.10549　Re: 事前事後デザインの分析方法について　　【波音】　2009/07/31(Fri) 21:09

ちょっと長くなるので分割して投稿しますが，体重(Weight)を体脂肪(Fat)と性別(Sex)で説明するような共分散分析モデルの解析例です。

> mydata # 使用するデータセット
   Weight Fat    Sex
1      89  28   Male
2      88  27   Male
3      66  24   Male
4      59  23   Male
5      93  29   Male
6      73  25   Male
7      82  29   Male
8      77  25   Male
9     100  30   Male
10     67  23   Male
11     57  29 Female
12     68  32 Female
13     69  35 Female
14     59  31 Female
15     62  29 Female
16     59  26 Female
17     56  28 Female
18     66  33 Female
19     72  33 Female

> # 交互作用項を含むモデルとして解析する
> result <- lm(Weight ~ Fat * Sex, data=mydata)

> # ダミー係数式の出力
> dummy.coef(result)
Full coefficients are 
                                   
(Intercept):    -44.60386          
Fat:             4.714976          
Sex:                 Male    Female
                  0.00000  57.37828
Fat:Sex:             Male    Female
                 0.000000 -3.073562

> attach(mydata)
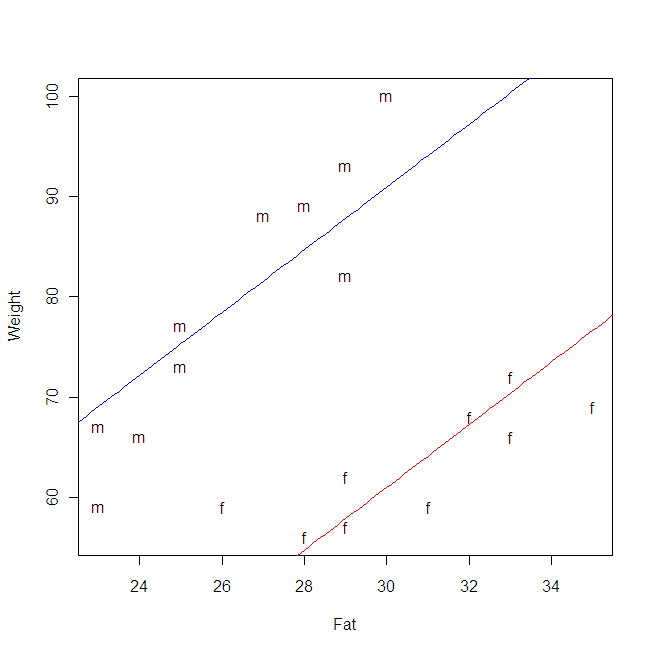
> plot(Fat, Weight, pch=c("m", "f")[Sex])
> x <- seq(20, 40, 0.1) # 直線を描くためのx軸のデータ
> mf <- -44.60 + 4.71*x # y軸のデータ(男性の)
> points(x, mf, type="l", col="blue") # 男性の回帰直線を描く
> ff <- -44.60 + 4.71*x + 57.37 - 3.07*x
> points(x, ff, type="l", col="red")

この結果が示す事実は，脂肪の増加に伴う体重の増加量は男性の方が女性よりも大きいということです(男性の傾きの方が大きい)。次のスレッドに示すように，加法モデルが当てはめられるときは，男性と女性の増加量に違いはないということになります。

No.10551　Re: 事前事後デザインの分析方法について　　【波音】　2009/07/31(Fri) 21:16 


> # 加法モデルの当てはめ
> add.model <- lm(Weight ~ Fat + Sex)
> dummy.coef(add.model)
Full coefficients are 
                                  
(Intercept):    -2.956024         
Fat:             3.131408         
Sex:                 Male   Female
                   0.0000 -29.9627

> plot(Fat, Weight, pch=c("m", "f")[Sex])
> mf2 <- -2.95 + 3.13*x
> points(x, mf2, col="blue", type="l")
> ff2 <- -2.95 + 3.13*x -29.96
> points(x, ff2, col="red", type="l")

あくまでも比較のための例示であって，今回のデータセットにおいて，この加法モデルを当てはめることは正しくありません。加法モデルが当てはめられる場合，増加量(傾き)は同じことになりますので，これが示す事実は男性と女性の違い(群間差)が認められるということです。
No.10552　Re: 事前事後デザインの分析方法について　　【波音】　2009/07/31(Fri) 21:18

加法モデルを当てはめた場合，2本の回帰直線は平行になりますね。

No.10556　Re: 事前事後デザインの分析方法について　　【好夫】　2009/07/31(Fri) 23:23

ありがとうございます。回帰直線の平行性という意味はよく分かりました。

ですが，共変数（プリテスト）と独立変数（条件：トレーニング実施と未実施）間にポストテストに対する交互作用があっても，そのまま共分散分析が可能ということになるのでしょうか？

例えば，SPSSで出てきたANCOVAによるTableから，条件の主効果が有意だったら，トレーニングの効果はあったと言えるのでしょうか？　

そ れと根本的な疑問ですがそもそも偏回帰係数が傾きだとすれば，相関係数と同じと考えると，プリテストとポストテストの関係はトレーニング効果で，トレーニ ングを受けてない方より逆に弱くならないのでしょうか。トレーニング効果があればあるほど傾きは平行には普通ならないと直感では感じるのですがどうでしょ うか？何か根本的な勘違いを私はしていますか？
No.10558　Re: 事前事後デザインの分析方法について　　【波音】　2009/08/01(Sat) 01:33

共変量というのは，私の例示でいえば性別という変数にあたるわけです。

まず好夫さんの解析しよう としているモデル式を書いてみることです(モデル式を書くことによって，自分が何をしたいのか確認できる)。そして，独立変数について，どの変数は連続型 で，どの変数はカテゴリカル型なのか(カテゴリカル型ならいくつの水準をもつのか)を整理してみましょう。

そうしていただけると，私もより正確な回答をさせてもらえると思います。

ちなみに，例示したデータ解析のモデル式は

Weight = Fat + Sex
(Fatは連続型，Sexは2水準のカテゴリカル型)
No.10562　Re: 事前事後デザインの分析方法について　　【好夫】　2009/08/01(Sat) 15:58

ありがとうございます。

おそらく

事後テスト＝条件＋事前テスト

条件は2水準（トレーニング実施群・未実施群）のカテゴリカル型，事前テストは連続型
共変量は，事前テストとなると思います。
No.10564　Re: 事前事後デザインの分析方法について　　【波音】　2009/08/01(Sat) 18:15

改めて前のスレッドにある

>　プリテストとポストテストの関係はトレーニング効果で，トレーニングを受けてない方より逆に弱くならないのでしょうか。

についてですが，そういう考え方も当然できます。しかし，それは実際に解析してみないと，その考察(考え方)が適切であるかどうかは分からないでしょう。

>　トレーニング効果があればあるほど傾きは平行には普通ならないと直感では感じる

その通りでしょう。「トレーニング効果があればあるほど」というのは，条件の水準に依存してテスト得点の増加量が多くなるということですからね。

ちなみに，

>　偏回帰係数が傾きだとすれば，相関係数と同じと考えると，

とありますが，正確には標準化偏回帰係数は相関係数と一致しますが，偏回帰係数と相関係数は一致しません。

---

>　共変数（プリテスト）と独立変数（条件：トレーニング実施と未実施）間にポストテストに対する交互作用があっても，そのまま共分散分析が可能ということになるのでしょうか？

すでに整理されているように，独立変数は条件(カテゴリカル型)と事前テスト(連続型)の2つですね。もし条件と事前テストの交互作用項が有意ならば，当てはめられる直線は並行ではなくなり，交互作用項が有意でなければ並行になるということです。

本を読むと，「共分散分析は回帰直線が平行である必要がある」的なことを書かれているものもありますが，そのようなことはないのです。直線が並行かどうかは交互作用があるかないかというだけのこと。

>　条件の主効果が有意だったら，トレーニングの効果はあったと言えるのでしょうか？

まず考えるべきことは，条件と事前テストの交互作用が認められたかどうかということです(どうでしたか？)。それとも，もしかしてSPSSでは共分散分析で交互作用項が出てこなかったりするのでしょうか・・・
No.10565　Re: 事前事後デザインの分析方法について　　【好夫】　2009/08/01(Sat) 22:47

>本を読むと，「共分散分析は回帰直線が平行である必要がある」的なことを書かれているものもありますが，そのようなことはないのです。

まさにこの点のみがネックになっています。私が調べた全ての本に書いてありますので。

＞まず考えるべきことは，条件と事前テストの交互作用が認められたかどうかということです(どうでしたか？)。

　有意になってしまったので，共分散分析はできないと悩んでいました。

＞それとも，もしかしてSPSSでは共分散分析で交互作用項が出てこなかったりするのでしょうか・・・

　手順として2段階に分け，まず，この平行性の検定をします。つまり交互作用を確認します。
No.10566　Re: 事前事後デザインの分析方法について　　【波音】　2009/08/02(Sun) 13:10

>　私が調べた全ての本に書いてありますので。

なぜ古典的な参考書に「回帰直線の平行性の検定」を事前に行うように書いてあるのかはよく分かりません(^_^;)

岩 崎「統計的データ解析入門　単回帰分析」東京図書(2006)を読んでみたら，どうやら2本の回帰直線の定数項(切片)の差の検定をすることが目的である として解説しているようです。実験計画の段階で2群の平均値の差の検定を行うことに着目するならば，たしかに2本の回帰直線は平行であると仮定されないと 定数項を比較することに意味はないですね。

>　有意になってしまったので，共分散分析はできないと悩んでいました。

前述したように，2本の回帰直線の定数項の差の検定を行うのであれば，傾きが異なる(交互作用が存在する)場合には不適切ということですね。しかし，繰り返しになりますが，交互作用項が有意ならばそれに応じた考察を行えばよいだけです。
No.10571　Re: 事前事後デザインの分析方法について　　【好夫】　2009/08/03(Mon) 11:02

丁寧な解説本当に感謝しています。

つまり

事後テスト＝条件＋事前テスト　

で交互作用があるわけですが，事前テストが素点で条件が上下となっています。
これに交互作用があるというのは，条件1の回帰直線と条件2の回帰直線が交差して
いるということですよね。これは，たとえば条件1が有効な場合とそうでない場合があるということでしょうか？そうだとすると，考察したいのは「有効なのはどの群なのか」ということになるのですが，それをこの後どうやって判別したらできるのでしょうか？
No.10581　Re: 事前事後デザインの分析方法について　　【波音】　2009/08/03(Mon) 21:14

>　交互作用があるというのは，条件1の回帰直線と条件2の回帰直線が交差しているということですよね。

そういうことになります。

>　条件1が有効な場合とそうでない場合があるということでしょうか？

改 めてNo. 10549の係数表について，これを条件1をMale，条件2をFemaleとして考えてみてください。Male（条件1: トレーニングあり）の傾きは4.71+0.00=4.71となり，Female（条件2: トレーニングなし）の傾きは4.71-3.07=1.64になります。これによれば，トレーニングありの傾きが大きいということは，トレーニングあり群の 方が事後テストでより大きな点数の増加があったということでしょう？

ただし，これはあくまでも一般的な例をあげての解釈ですから，実際にどのように結果を考察するかというのは分析者によるわけです（これ以上のことは実際の解析結果を見ていない私にはわかりません＾＾；）。

> dummy.coef(result)
Full coefficients are 
                                   
(Intercept):    -44.60386          
Fat:             4.714976          
Sex:                 Male    Female
                  0.00000  57.37828
Fat:Sex:             Male    Female
                 0.000000 -3.073562
No.10582　Re: 事前事後デザインの分析方法について　　【好夫】　2009/08/04(Tue) 06:48

ありがとうございます。だいぶすっきりしてきました。

事前テスト得点をX軸，事後テストをY軸にした場合

交 互作用がなく，トレーニング効果がある場合は，そのまま回帰直線は平行にトレーニング前より上に上がったところに引かれ，何の問題もなくその差を検定して （事前テスト下位群・上位群関係なく）トレーニング効果ありとなりますが，交互作用があってトレーニング効果があるとなった場合は，おそらく?「事前テス トの下位群に効果があるが，上位群にはあまりない」?「事前テストの上位群に効果があるが，下位群にはあまりない」となり，?の場合は傾き（偏回帰係数） は逆に小さくなり，?の場合は傾き（偏回帰係数）が大きくなるという考察がありえるということですね。
No.10584　Re: 事前事後デザインの分析方法について　　【波音】　2009/08/04(Tue) 09:23

基本的にそういう解釈で間違いないと思います。

（ちなみに，この掲示板内に限らず丸付き文字のような機種依存文字は使わない方が無難だと思います。私もWindowsユーザですが，日本のようにWindowsユーザが大半の世間ではあまり気にされないようですが・・・）
No.10588　Re: 事前事後デザインの分析方法について　　【好夫】　2009/08/04(Tue) 16:33

波音さん

本当にありがとうございました。
何とか考察できる気がしてきました。
やはり使う分析方法の根本の理屈が分からないと，統計は意味がないですね。

追伸：
丸付き文字とか気をつけます。

今後ともご指導よろしくお願いします。

好夫

● 「統計学関連なんでもあり」の過去ログ--- 042 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る