「統計学関連なんでもあり」の過去ログ--- 042

No.10103　多変量回帰分析と主成分分析　　【波音】　2009/06/17(Wed) 15:53

正準相関分析が，第1変数群をY = {y1, y2, ..., yi}とし，第2変数群をX = {x1, x2, ..., xj}として，

　Y = X

というモデルで表せるとしたら，これは第1変数群Yと第2変数群Xそれぞれに対して主成分分析を行って，その主成分（合成変数）同士の相関を見ることと同義とはいえないでしょうか。

Yについて主成分分析を行って得られた第1主成分の主成分得点をz1，Xについて主成分分析を行って得られた第1主成分の主成分得点をz2とした場合，

　z1 = z2

とした回帰モデルを解析することと意味的には似たようなことをやっているかのように思えるのですが？

また，多変量回帰分析（これは正準相関分析といえる？）：

　y1, y2, y3 = x1 + x2 + x3

というモデルを解析することは，変数群{x1, x2, x3}について主成分分析を行い，合成変数zを作り出し，これを説明変数として：

　y1 = z
　y2 = z
　y3 = z

という3通りの単回帰モデルを解析することとは別物なのでしょうか？

No.10118　Re: 多変量回帰分析と主成分分析　　【青木繁伸】　2009/06/17(Wed) 21:54

条件を定めてテストデータを生成して，実際に両方の方法で分析してみて結果を比較すれば解答が得られると思います。
数式で結果を導くことも可能でしょう（両方の結果の明示的な関係性を示すことができるでしょうからね）。
明示的な関係を示すことはできなくても，どの程度の近似性があるかを示すことは意義があることだと思います。
是非やってみて，結果を教えてください。

No.10130　Re: 多変量回帰分析と主成分分析　　【波音】　2009/06/18(Thu) 17:21

set.seed(123)

X <- matrix(rnorm(60), 20, 3)*10+50 # 第1変数群
Y <- matrix(rnorm(60), 20, 3)*10+80 # 第2変数群

青木先生の本(http://aoki2.si.gunma-u.ac.jp/R/Rstat-support.html)にあるcancor2()を使って正準相関分析を行う。

cancor2(X, Y)

Xの第1正準変量をf，Yの第1正準変量をgとすると，以下のような式が得られる(標準化係数)。

f = 0.31*x1 - 0.70*x1 + 0.71*x3
g = - 046*y1 - 0.97*y2 + 0.13*y3

この式より得られる正準得点f.scoreとg.scoreの相関係数が正準相関係数であり，これは0.66であることが解析結果から分かる。

f.score <- cancor.result$xscore[,1]
g.score <- cancor.result$yscore[,1]
cor(f.score, g.score)

f.scoreを応答変数，g.scoreを説明変数とした単回帰モデルを解析してみる。

plot(f.score, g.score)
summary(lm(f.score ~ g.score))

以上より，f = - 12.88 + 0.66 * gという回帰方程式が得られる。

さて一方で第1変数群に対して主成分分析を行い，新たな合成変数(主成分)を作り出してみる。

result1 <- princomp(X, cor=TRUE)
summary(result1, loadings=TRUE)

第1主成分は　zx = 0.592*x1 - 0.537*x2 - 0.601*x3　である。

同様に第2変数群に対しても：

result2 <- princomp(Y, cor=TRUE)
summary(result2, loadings=TRUE)

これの第1主成分は　zy = 0.385*y1 - 0.675*y2 - 0.629*y3　である。

zx <- result1$scores[,1]　#zxの主成分得点
zy <- result2$scores[,1]　#zyの主成分得点
plot(zx, zy)
cor(zx, zy) # 2つの主成分得点は無相関であることが分かる
[1] 0.04860079
summary(lm(zy ~ zx))

lm(zy ~ zx)より　zy = 0 + 0*zx　という回帰式が得られる。

結局，正準相関分析の結果と第1変量群の主成分と第2変量群の主成分の相関を見た場合，両者は全く異なる結果が得られることが分かった。

No.10131　Re: 多変量回帰分析と主成分分析　　【波音】　2009/06/18(Thu) 17:43

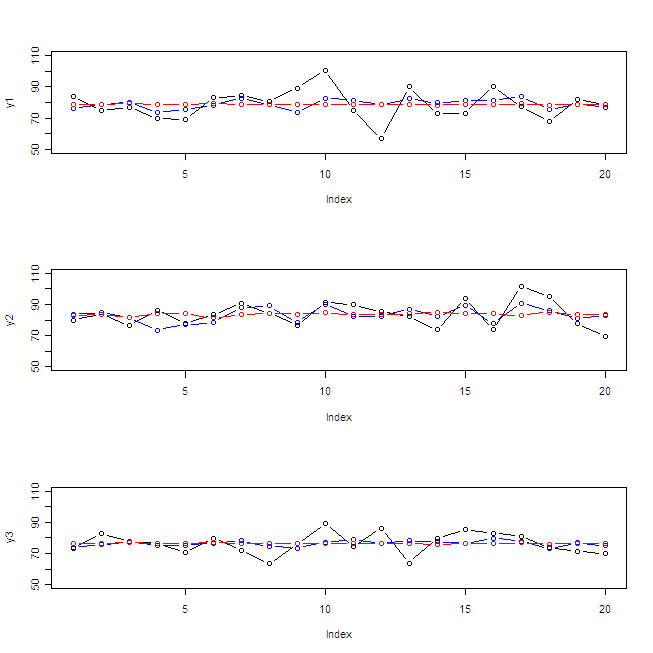
X = {x1, x2, x3}という変数群に対して主成分を求め，それを説明変数としてy1 = zx, y2 = zx, y3 = zxとすることはかなり予測精度が落ちるので好ましい方法ではないことが分かりました。
> y1 <- Y[,1]
> y2 <- Y[,2]
> y3 <- Y[,3]
> summary(lm(y1 ~ zx))
> summary(lm(y2 ~ zx))
> summary(lm(y3 ~ zx))
Rで多変量回帰を行う関数を見つけられなかったのでLISREL(http://www.ssicentral.com/)を用いて多変量回帰モデルとして解析。多変量回帰モデルの解析によって得られたy1, y2, y3それぞれの重回帰モデルの予測精度と比較してみる。

# 多変量回帰モデルから得られたy1の予測式
lm.y1 <- function(x1, x2, x3) 65.62 + 0.13*x1 + 0.30*x2 - 0.16*x3

# lm(y1 ~ zx)より得られたy1の予測式
pca.y1 <- function(zx) 78.801 + 0.293*zx

# 実測値y1のプロット
plot(y1, type="b", ylim=c(50, 110))

# 多変量回帰の予測値プロット
points(lm.y1(x1, x2, x3), type="b", col="blue")

# 主成分を説明変数としたモデルの予測値プロット
points(pca.y1(zx), type="b", col="red")

以下，y2とy3も同様。

lm.y2 <- function(x1, x2, x3) 93.80 - 0.21*x1 + 0.38*x2 - 0.36*x3
pca.y2 <- function(zx) 83.7509 - 0.8128*zx
plot(y2, type="b", ylim=c(50, 110))
points(lm.y2(x1, x2, x3), type="b", col="blue")
points(pca.y2(zx), type="b", col="red")

lm.y3 <- function(x1, x2, x3) 61.68 + 0.16*x1 + 0.14*x2 - 0.0098*x3
pca.y3 <- function(zx) 76.4062 + 0.3165*zx
plot(y3, type="b", ylim=c(50, 110))
points(lm.y3(x1, x2, x3), type="b", col="blue")
points(pca.y3(zx), type="b", col="red")