No.09132 Re: y=x^3の関係をGLMで解析 【青木繁伸】 2009/02/05(Thu) 15:51
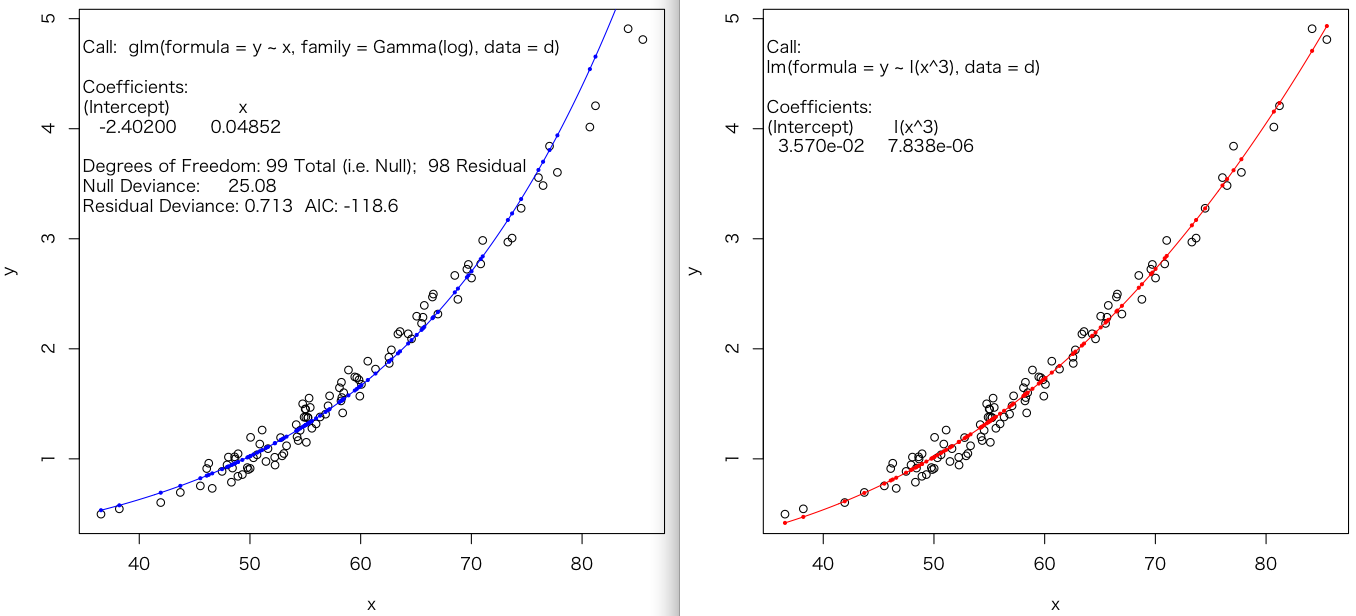
glm(y~x, d, family=Gamma(log)) と lm(y~I(x^3), d)
の比較をしてみました。glm(y~x, d, family=Gamma(log)) が,実際は何をしているか,ちょっと調べないとわかりませんが。
set.seed(1234)図をクリックすると,原寸で表示します
x <- rnorm(100, mean=60, sd=10)
y <- jitter(x^3/50^3, amount=0.2)
d <- data.frame(x=x, y=y)
ans.lm <- lm(y~I(x^3), d)
summary(ans.lm)
plot(y~x)
x2 <- seq(min(d$x), max(d$x), length=1000)
d2 <- data.frame(x=x2)
y2 <- predict(ans.lm, newdata=d2)
lines(x2, y2, col="red")
points(fitted.values(ans.lm)~d$x, pch=19, cex=0.4, col="red")
strings <- capture.output(ans.lm)
text(34, seq(4.9, 2.9, by=-0.18)[1:7], strings, pos=4)
#
ans.glm <- glm(y~x, d, family=Gamma(log))
summary(ans.glm)
plot(y~x)
x2 <- seq(min(d$x), max(d$x), length=1000)
d2 <- data.frame(x=x2)
y2 <- predict(ans.glm, newdata=d2)
lines(x2, exp(y2), col="blue")
points(fitted.values(ans.glm)~d$x, pch=19, cex=0.4, col="blue")
strings <- capture.output(ans.glm)
text(34, seq(4.9, 2.9, by=-0.18)[1:10], strings, pos=4)