No.08683 Re: 順序尺度と中心極限定理 【青木繁伸】 2008/12/19(Fri) 10:31
> 1．各項目の得点は，もともと順序尺度なのだし，正規分布しないだろう。
> 2．その合計点は，正規分布に近づくだろう。
> 3．正規分布に近ければ，パラメトリックな解析をしていいだろう
> と言うことだと思いますが，1．と2．のつながりが理解できない
> 「母集団からとった標本の平均値の分布は，正規分布にほぼ従う。たとえ母集団が正規分布であろうとなかろうと」と理解しています
ということですが，「標本の平均値の分布」も，「標本の和の分布」も正規分布に従うのですよね。前者は後者を定数で割っただけのものですから。
つ いでに，0，1，2の乱数を5個発生させ合計を取るというのを5000回行って，つまり，5000個の和の度数分布を描くと添付図のようになります。正規 分布に近いと言えば近いように見えますが，シャピロ・ウィルクの正規性検定では，正規分布ではないという結論になります。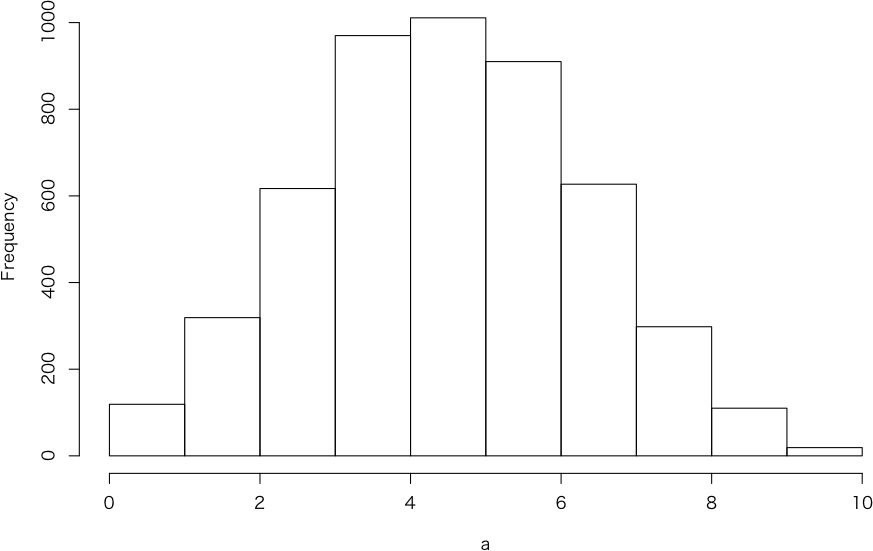
No.08685 Re: 順序尺度と中心極限定理 【オオモリ】 2008/12/19(Fri) 10:55
早速のお返事ありがとうございます。
ああ，もう少しで分かりそうなのですが，実は分かっていません。なにか指先に引っかかった感じ（比喩）はするのですが・・・・。
《「標本の平均値の分布」も，「標本の和の分布」も正規分布に従う》，おお，それはそうですね。理解しました。
結局，私が理解できないのは，中心極限定理の「意義」が分かっていないのだと思うのですが。。。。。
たとえば，10項目（各項目は0点〜4点）からなる，Y-BOCSという強迫性障害の評価尺度があります。これを100人の患者さんに行ったとします。
ここで標本の平均値，というのは，標本(n=100)のmeanですよね。これが30点だったとします。
標本の和というのは30×100＝3000ですね。
同じようにまた別の100人からデータをとって，このときの標本平均は28点（和は2800点）だったとします。
同じように何回も，別々の100人からデータをとったとき，それぞれの標本平均の分布（標本の和の分布）が，正規分布に従うってことですよね。
意味は理解できていると思うのですが・・・・・・。
で，ここから分からなくなるのです。上記のことと，1．と2．のつながりが。なにか基本的なことが理解できていないような気がします。
統計の本を何度読んでも，中心極限定理の意味はわかるのですが，意義が理解できないのです。
「母集団」からとった「標本」の「平均値（和）」の分布は正規分布に従う。
は
「一人の患者さん」からとった「各項目」の「平均値（和）」の分布は正規分布に従う。
と等価ですか？
No.08689 Re: 順序尺度と中心極限定理 【青木繁伸】 2008/12/19(Fri) 12:40
> たとえば，10項目（各項目は0点〜4点）からなる，Y-BOCSという強迫性障害の評価尺度があります。これを100人の患者さんに行ったとします。
> ここで標本の平均値，というのは，標本(n=100)のmeanですよね。これが30点だったとします。
> 標本の和というのは30×100＝3000ですね。
違いますよ。
一人の患者の10項目への評価得点の和ですよ。
挙げられた例では0〜4点を取る10項目の和です。
中心極限定理では，たとえ各項目で0〜4の得点の分布がどうであろうと（例えば一様分布であろうと）そのようなものを10項目分合計すれば，その合計得点は標準正規分布に従うということ。
100人の患者の合計得点それぞれが標準正規分布に従うので，ヒストグラムを描くと正規分布に近似できそうな分布曲線になるということ。
No.08701 Re: 順序尺度と中心極限定理 【オオモリ】 2008/12/19(Fri) 21:59
理解の悪い初心者にもう少しつきあっていただけますか。
もう少し，で分かります。
中心極限定理のもともとの意味からすると，
statement A「母集団からランダムサンプリングして得られた100人の患者の，ある心理尺度の評価得点（合計点）の平均（n=100)の分布は正規分布に従う」んですよね。
■質問1■
この理解そのものも違ってますか（理解していたつもりなのに自信が無くなってきた）。
さらに，この中心極限定理を，順序尺度を間隔尺度として扱うことの根拠として適用すると，
statement B「ある一人の患者に対して行った心理尺度の，各項目の評価得点の平均もしくは和（n=10。ここでは人数ではなく尺度の項目の数)は，(標準）正規分布に従う」.
■質問2■
statement Aとstetement B は統計学的に同じことを言っているのですか？
つまり，
A「母集団」とB「一人の患者」
A「100人の患者の合計点の平均」とB「一人の患者における，各項目の評価得点の平均点もしくは和（項目数10）」では，意味が違うような気がするのですが，どうでしょうか？
No.08702 Re: 順序尺度と中心極限定理 【青木繁伸】 2008/12/19(Fri) 22:12
何を母集団として，何を標本としているかのところで，食い違いがあるのでしょうね。
わかりやすい例を出しておきましょう。
10円玉を20個一度に投げます。表が出た個数を記録します。
この実験を1000回やります。
表の出た回数の1000個の記録のヒストグラムを描きます。
そのヒストグラムは，正規分布で近似できます。
1個の10円玉に関して，表が出るのも裏が出るのも半々で，一様分布です。
20個の10円玉の表が出た回数は，中心極限定理により正規分布に近似されます。
この場合，表裏が半々であるというのが母比率が0.5という母集団です。
そこから，20個の標本を採るというのが，20個の10円玉の裏表を観察するということです。
表の出た回数というのが，標本統計量です。
1000回やってみるというのが，試行です。
その分布をとるというのが，経験的分布です。
この段階の標本統計量は，例えば身長というデータなら，個人の身長ということ。個人の身長は，母の遺伝子だの父の遺伝子だの肉をどれくらい食うだの野菜をどれくらい食うだの諸々の要因の集大成（まさに中心極限定理の結果）である一つにの実現値。
で，普通の測定値の段階では，その測定値がどんな生成機序によって出来ているかは余り考えません。考えないけど，色々な条件が関与しているから，正規分布に近くなることが多いのではないかなという，かすかな期待があるんでしょう。
もう一段中間にある。
この段階では，前段階のようなデータ発生機序があったとしてそれを実際に複数セット観察するという段階。
20回中の表の回数も，ばらつくだろうけど，それが500セット分くらい観察されるとバラツキも更に小さくなるだろうと言うこと。
身長のデータ例なら，実際にn人を調査して実際の身長の分布を観察する段階。
更に中心極限定理が働いてより正規分布に近いデータが観察されるだろうということ。
さ て，そのような条件で得られるデータ（つまり，母比率0.5の20個のデータを取って，表の出た個数がデータ）を例えば500回分やって，その平均値（合 計）の分布を見るというのが，「標本統計量の統計量の分布」を考えるという段階。これは，期待値は同じであることが期待できるが，その散らばりは遙かに小 さい。
この段階での対象は，母集団から標本を採って平均値を求めるということをまた何回も繰り返すと，身長の平均値の平均値や標準偏差（もはや， 標準偏差ではなく標準誤差と呼ばれるもの）を考えるレベルになっているわけです。標本の平均値は母平均と同じくらいになるだろうけど，平均値の標準偏差 （標準誤差）は，母標準偏差を標本の大きさの平方根で割ったものになるのです。
まとめると，個体のレベルで観察されるデータにも中心極限定理が働く，
複数の個体について統計量を求めるときにも中心極限定理が働く，
そのような標本調査を繰り返すときにも中心極限定理が働く，
と，まあ，3段階あるということ。普通は，最初の段階は数えていない。
第2段階が1回の標本調査で得られるデータの分布を考察する段階，
第3段階がその1回のデータの標本値はどのような分布になるかを考察する段階（平均値の平均値や標準偏差（標準誤差）を考える）。
ややこしいですね〜。
ちなみに，20個のサイコロをふって，出た目の数を記録するという実験も同じような結果を生み出すでしょう。
No.08708 Re: 順序尺度と中心極限定理 【オオモリ】 2008/12/20(Sat) 10:24
分かった。分かった。分かりました。まさしくAch-so-erlebnis！（アハ体験）。
数学がよく分からないので，具体的な例だと感じがつかめてなっとくできます。
身長の例，3段階のこと，納得しました。
数年来の胸のしこりがとれたような気がします。
数学的には理解していないので本当に分かったとは言えないのでしょうが，とりあえずは，これでいいことにします。
うーん，聞いて良かった。実に気分がよい！
こういう説明をきちんとしてある統計の教科書ってあるんだろうか・・・・
また，書き込みます。
ありがとうございました。
● 「統計学関連なんでもあり」の過去ログ--- 042 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る