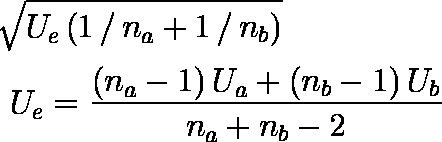a <- NULL
set.seed(1);a[1:100] <- rnorm(100,2,2);
a[101:200] <- rnorm(100,4,2);
a[201:300] <- rnorm(100,20,2)#生データの作成
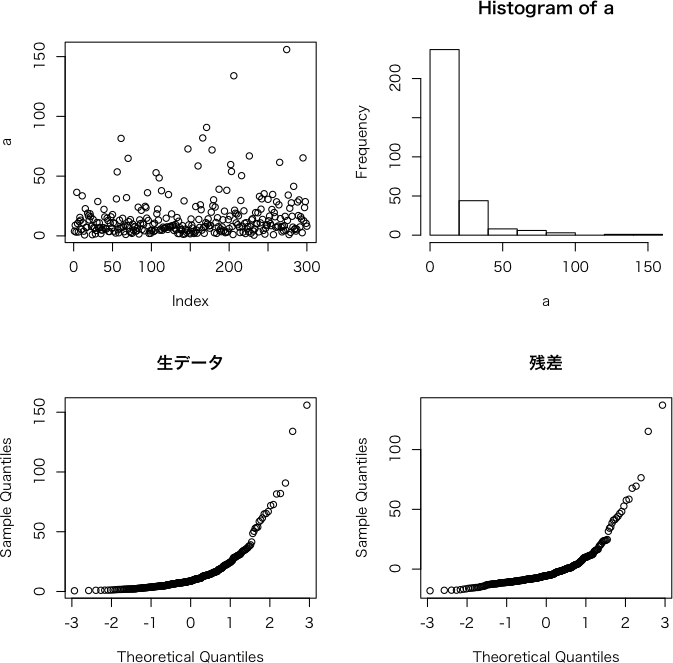
par(mfrow=c(2,2));plot(a);hist(a);qqnorm(a,main=("生データ"))#データ概観。明らかに正規分布ではなさそう
shapiro.test(a)#正規性の検定。やっぱり生データは正規分布ではなさそう
b <- rep(c(2,4,20),each=100)
c <- lm(a~as.factor(b))#解析をして誤差を抽出
qqnorm(resid(c),main="残差")
shapiro.test(resid(c))#誤差は正規分布でありそう
summary(c)#生データが正規分布でなくても綺麗に推定できているようです。

---

No.08617　Re: 生データが正規分布だったら誤差も正規分布？　　【Sai】　2008/12/12(Fri) 12:15

>set.seed(1);a[1:100] <- rnorm(100,2,2);
>a[101:200] <- rnorm(100,4,4);
>a[201:300] <- rnorm(100,20,8)#生データの作成

これは等分散性の仮定を崩すということでしょうか？実際に言われたとおりにやってみたところ，shapiro.testの結果が生/残差の両方とも正規分布と同じとはいえない，という結果が返ってきました。

set.seed(1);a[1:100] <- rnorm(100,2,2);
a[101:200] <- rnorm(100,4,4);
a[201:300] <- rnorm(100,20,8)#生データの作成
shapiro.test(a)
shapiro.test(resid(c))
mean(resid(c));var(resid(c));hist(resid(c))

残 差の平均値も0付近で，分散はやや大きいものの正規分布の形をしていると思うのに，何故こんな結果が返ってくるのでしょうか？shapiro.testに ついて何か思い違いをしているのかもしれません。等分散であることと生データと残差の誤差の関係は一体…とここまで書いて青木先生の記事が消えていました ^_^;この方向で合っていますか？

---

No.08618　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 12:24

ちょっと迷っていたので，前の記事は削除してしまいました。

呈示されたシミュレーション結果がな にを主張しようとしているのかちょっと不明。つまり，「分散分析の仮定は誤差が正規分布であること」と「生データが正規分布でないからといって誤差も正規 分布でないということはないと思う」と「解析時に生データが正規分布に従っている必要がある」との関連がよくわからない。

母分布に対数正規分布を使った場合の例

set.seed(1)
a <- c(rlnorm(100,2), rlnorm(100,2.2), rlnorm(100,2.4)) #生データの作成

---

No.08619　Re: 生データが正規分布だったら誤差も正規分布？　　【Sai】　2008/12/12(Fri) 13:21

　すいません，私もよくわからなくなってしまったので，少し整理させてください。
疑問の発端は私の周りの人が生データの分布形をみてどのような分析をするか決めているようだったので，本当に生データから分析の種類を決めてよいのかと思ったのがそもそもでした。
　 その人たちの主張としては，正規性の検定を行って生データが正規分布に従ってなければ対数変換を行って正規分布に直し，分散分析や回帰分析を行ってその有 意性を見るというものです。しかし「分散分析の仮定は誤差が正規分布であること」だと私は思っていたので，その人たちの持っている「生データが正規分布で ないからといって誤差も正規分布でないということはない」と思ったのでした(私が最初に示したプログラムがそれです。生データは正規分布ではないですが， 誤差は正規分布です)。だから誤差さえ正規分布であれば分散分析などを使えるのではないか，と思い検証したかったのです。もし誤差さえ正規分布であればよ いのであれば，その人たちが言うように「解析時に生データが正規分布に従っている必要」はないと思うのです。

青木先生が示してくださった 対数正規分布の例ですが，これは対数のまま解析してみて，誤差が正規分布じゃないなら対数変換をしなさい，という意味ですか？つまり生データが正規分布で ある必要はないが，「解析の結果」，残差が変な形をしているようであれば生データを対数変換して解析を行いなさいということでしょうか？完全に私の推理な ので間違っていると思いますが…。

a <- NULL
set.seed(1);a <- c(rlnorm(100,2), rlnorm(100,2.2), rlnorm(100,2.4)) #生データの作成
par(mfrow=c(2,2));plot(log(a));hist(log(a));qqnorm(log(a),main=("生データ"))#データ概観。
b <- rep(c(2,4,20),each=100)
c <- lm(log(a)~as.factor(b))
qqnorm(resid(c),main="残差")
summary(c)

で すが，私が言いたかったのは最初に私が示したプログラムのように，見た目が正規分布でなくても，やってみたらうまくいくことがあるのだから，生データが正 規分布でないからといっていつでも対数変換orノンパラという考えは違うのではないかなぁということです。ですから，正規性の検定は生データに対してでは なく，残差に対して行うことで，分散分析が使えるのかどうかが判断できると思うのですが，いかがでしょうか。ひょっとすると多重性の問題にあたるのかもし れませんが…。

---

No.08620　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 14:20

念のために本を引っ張り出してきて，一元配置分散分析の仮定について，Fixed moded のとき，分散比が F 分布に従うためには
(1) k 標本は互いに独立（独立標本）
(2) 標本は正規分布に従う（したがって，母分布も正規分布）
(3) 標本分散に有意差がない（したがって，母分散は等しい）
(4) 帰無仮説が正しい
F 値が有意に大きいと，上の4つのいずれかが正しくないことを示している。一般には(4)が否定される。そのためには(1)〜(3)のいずれも正しくなければならない。ただし，(2)，(3)については頑健性がある。

ということで，「分散分析の仮定は誤差が正規分布であることですよね」というのは，間違いだと思いますよ。

変 数変換をする意義は，平均値と分散が等しい（つまり平均値の差があるなら，分散の差がある）ポアソン分布とか，対数をとると正規分布になる対数正規分布， などなどへの対処のため。一般に標本サイズは小さいことがあるので，標本が正規分布に従うかどうかは判定が難しい。理論的に考えて母分布がどのようなもの であるか考えるべし。そして，そのような分布を仮定するのが難しいときには，分布によらない方法（ノンパラメトリックな方法）も考えましょうと言うこと。

---

No.08621　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 14:46

「正規性の仮定」をどうとらえるかによって，分布が正規分布でなければならないのか，誤差が正規分布なのかである が，後者は Mean1 - Mean2 の誤差分布が正規分布という言う意味で使っているのなら取るに足りないことを言っていると思う。平均値の誤差は中心極限定理で正規分布に従う（サンプルサ イズが小さい場合はt分布）のだから，母分布がどんなものであっても平均値の差の分布は正規分布に近似される。

本質的には，母分布が正規分布でなければならないということでは？ポアソン分布や二項分布，対数正規分布など。

> a <- matrix(runif(1000000), 1000)
> b <- matrix(runif(1000000, max=2), 1000)
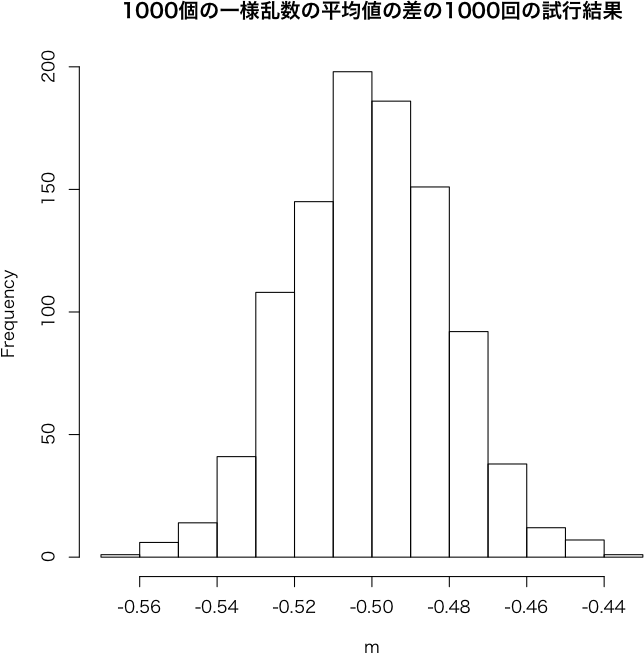
> m <- colMeans(a)-colMeans(b)
> hist(m, main="1000個の一様乱数の平均値の差の1000回の試行結果")
> shapiro.test(m)
シャピロ・ウィルクの正規性検定

データ:  m 
W = 0.9991, P値 = 0.9336

母分布が対数正規分布で，サンプルサイズが小さいときには，平均値の差の分布は正規分布とはいえないというようなことが多くなる。

> a <- matrix(rlnorm(100000), 50)
> b <- matrix(rlnorm(100000,0.3), 50)
> m <- colMeans(a)-colMeans(b)
> shapiro.test(m)
シャピロ・ウィルクの正規性検定

データ:  m 
W = 0.9962, P値 = 6.728e-05

同じような条件で，母分布が一様分布なら，平均値の差の分布は正規分布で近似できる

> a <- matrix(runif(100000), 50)
> b <- matrix(runif(100000,0.3), 50)
> m <- colMeans(a)-colMeans(b)
> shapiro.test(m)
シャピロ・ウィルクの正規性検定

データ:  m 
W = 0.9994, P値 = 0.8067

母分布が正規分布なら，当然

> a <- matrix(rnorm(100000), 50)
> b <- matrix(rnorm(100000,0.3), 50)
> m <- colMeans(a)-colMeans(b)
> shapiro.test(m)
シャピロ・ウィルクの正規性検定

データ:  m 
W = 0.9992, P値 = 0.6051

---

No.08622　Re: 生データが正規分布だったら誤差も正規分布？　　【Sai】　2008/12/12(Fri) 15:11

私の調べた限りですが，例えば"「生物統計学入門」山田作太郎，北田修一共著"という本の93ページから分散分析の章が掲載されています。その中で，t検定と分散分析を関連付けた説明がありますので，引用します。

引 用)t検定を使うことができるのはそれぞれの母集団が正規分布N(u1,s^2)，N(u2,s^2)に独立に従っている場合である。つまり，分散は等し いが，平均だけが違っている場合を想定して，帰無仮説u1=u2を適当な対立仮説に対して検定する。分散分析はこれを3つ以上の母集団の場合に拡張したも のである。すなわち分散分析とは3群以上の母集団がそれぞれ分散が等しい正規分布に従う場合の母平均の差の検定のことをいう。(引用終わり)

ここで問題となるのはs^2です。このs^2は誤差に他ならず，それはY=a(切片)+b(傾き)X+e(誤差分散)のeで表されていると理解しております。
つまり，(1/(n-1))*sum((Yi-Y)^2)で表される分散ではないということです。

ですから私としましては逆に分散分析は誤差が正規分布であることを仮定していると理解しているのですが…。そしてこれはMean1 - Mean2 の誤差分布ではないと思います。s^2は1自由度あたりの群内分散であると理解しています。

例 えばRのglm関数でもfamilyというところで，poisson, gaussian, binomialなどを決めることができますが，それはこのeの分布についての仮定であると理解しています。実際eの分布がgaussianのときに glmはlmやaovと全く一緒の結果を返すのはそういうわけだと思っておりましたが…。

そして，今回私が示したプログラムでも母集団は正規分布をしておりませんが，これはこのまま分散分析してはいけないデータなのでしょうか？

---

No.08623　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 15:24

> このs^2は誤差に他ならず，それはY=a(切片)+b(傾き)X+e(誤差分散)のeで表されていると理解しております。

> つまり，(1/(n-1))*sum((Yi-Y)^2)で表される分散ではないということです。

(1/(n-1))*sum((Yi-Y)^2) というのはどこから出てきましたか？そんなもの使いませんよ。

二群の平均値の差の検定のt統計量。分子は平均値の差（の絶対値），分母（標準誤差）は添付画像の上の式，その中のUeは下の式。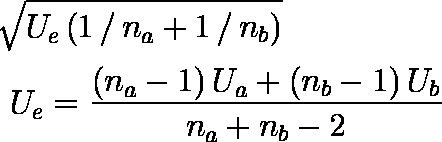

---

No.08624　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 15:34

一元配置分散分析の分散比の分母は群内平均平方

---

No.08625　Re: 生データが正規分布だったら誤差も正規分布？　　【Sai】　2008/12/12(Fri) 16:34

えっと，まず8623ですけれども
>(1/(n-1))*sum((Yi-Y)^2) というのはどこから出てきましたか？そんなもの使いませんよ。
使わないのは承知しているのですが，生データの分散ではないですよね，という確認のために載せただけです。誤解を招いてしまったようで失礼しました。
8624の群内平均平方(Vw)がまさに群内分散ですね。私はこれがeにあたるのだと理解しております。そしてこれが正規分布の必要があると理解しています。繰り返しになりますが，私が一番最初に示した生データに分散分析を行うのは間違っているのでしょうか？

---

No.08626　Re: 生データが正規分布だったら誤差も正規分布？　　【青木繁伸】　2008/12/12(Fri) 18:22

最初の質問で，回帰分析とか誤差分散とか話がよく見えなかったのですけど，結局の所は，呈示されたデータ例で分散 分析（一元配置分散分析）を行って良いものかどうかということなんですね。そして，その疑問は全体をまとめた（300個の）データが正規分布しないんだけ どということですか？

一元配置分散分析が仮定することについて No.8620 に書きましたけど，データ全体が正規分布するかどうかじゃないですよ。個々の標本（標本群）ごとに，データは正規分布に従う。平均値は標本ごとに違うが分 散は同じということです。教科書的には，独立k標本の分散の等質性はバートレットの検定を行います。それで等質性が確認されたら一元配置分散分析を行って 良いということ。（標本ごとに正規分布に従うかどうかはあまり検定されませんね。サンプルサイズが小さいと正規分布するという帰無仮説が採択されがちであ ることと，非正規性に対しては頑健性があることに頼るため）。

で，まあ，各標本ごとに正規性の検定をしてみましょう

> c<- matrix(a,100)
> b <- rep(1:3, each=100)
> apply(c, 2, shapiro.test)
[[1]]

	Shapiro-Wilk normality test

data:  newX[, i] 
W = 0.9956, p-value = 0.9876

[[2]]

	Shapiro-Wilk normality test

data:  newX[, i] 
W = 0.9743, p-value = 0.04763

[[3]]

	Shapiro-Wilk normality test

data:  newX[, i] 
W = 0.9889, p-value = 0.5793

まあ，第2群が正規分布に従わないということになりましたが，0.05ギリギリなので，見逃してやりましょう。次に，バートレット検定

> bartlett.test(a, b)

	Bartlett test of homogeneity of variances

data:  a and b 
Bartlett's K-squared = 1.9708, df = 2, p-value = 0.3733

めでたく，分散は一様であるとのご託宣が出たので，一元配置分散分析をやってみる。

> oneway.test(a~b, var.equal=TRUE)

	One-way analysis of means

data:  a and b 
F = 2601.876, num df = 2, denom df = 297, p-value < 2.2e-16

な お，var.equal=TRUE は，「分散は等しい」との仮定を oneway.test に伝えるもの。R の oneway.test は，独立2標本の平均値の差の検定（t検定）におけるウェルチの方法を拡張した，等分散性が仮定できないときの一元配置分散分析をするほうがデフォルトに なっている。

> oneway.test(a~b)

	One-way analysis of means (not assuming equal variances)

data:  a and b 
F = 2435.060, num df = 2.000, denom df = 197.355, p-value <
2.2e-16
まあ，こんな風です。