No.07866　一般線形モデルの固定因子について　　【ねじきん】　2008/10/08(Wed) 10:58

一般線形モデルの固定因子には3群以上の質的なデータも投入してよいでしょうか？
重回帰モデルやロジスティック回帰モデルでは，3群以上の質的データはダミーコード化されることが多いと思います。
重回帰モデルやロジスティック回帰モデルでは，「回帰係数が0である」を帰無仮説としてそれぞれの独立変数が検定されますが，一般線形モデルの各独立変数に対する有意水準の帰無仮説は何になりますか？

私は一般線形モデルの時も3群以上の質的データはダミーコード化するものだと思っていたのですが，今日，職場の方と話していて，自分の考えが間違っているような気がしてきました。
一般線形モデルの固定因子の帰無仮説は分散分析のように「固定因子の群間に差がない」なのかなと思っています。
教えてください。

統計ソフトはSPSSを使用しています。
No.07869　Re: 一般線形モデルの固定因子について　　【波音】　2008/10/08(Wed) 15:37

>　一般線形モデルの固定因子には3群以上の質的なデータも投入してよいでしょうか？

問題ないでしょう。

1要因の分散分析モデルのモデル式は次のようになります。

　　　Y = X1

X1の水準（カテゴリ，属性，群）が2つだろうと，3つ以上だろうと問題なく扱えるでしょう。

>　重回帰モデルやロジスティック回帰モデルでは，3群以上の質的データはダミーコード化されることが多いと思います。

重回帰モデルは

　　　Y = X1 + X2 + ... + Xn

で表され，独立変数X1, X2, ..., Xnはいずれも連続型である場合です。したがって，重回帰モデルではダミー変数を用いる必要はありません（ダミー変数を用いるのはカテゴリカル型の変数である場合です）。

また，ロジスティック回帰モデルは従属変数Yが2値データであるというだけで，独立変数の扱いは（根本は）同じです。

ちなみに，一般線形モデルというのは分散分析モデル（独立変数がカテゴリカル型），回帰分析モデル（独立変数が連続型），共分散分析モデル（独立変数にカテゴリカル型と連続型が混在）などのモデルをまとめて"一般線形モデル"としているわけです。

これを拡張した一般化線形モデルでは従属変数が2値データ（ロジスティック回帰モデル）でもカテゴリカル型でも扱えるわけです。
No.07882　Re: 一般線形モデルの固定因子について　　【ねじきん】　2008/10/09(Thu) 09:09

書き込みありがとうございます。

なるほど・・・と思ったのですが，確認させてもらいたいことがあります。

>　重回帰モデルではダミー変数を用いる必要はありません（ダミー変数を用いるのはカテゴリカル型の変数である場合です）。

ということは，カテゴリー型の変数を独立変数としたい場合はダミー変数にする必要があると理解していいですか？
そうしないと，たとえば，職業を示す変数（1営業，2主婦，3管理職，4事務職）などには順序もないし，間隔もないので，そのまま投入すると変な結果になりますよね？

このようなカテゴリー型の変数は，重回帰やロジスティック回帰の時にはダミーコード化して，一般線形モデルの時にはダミーコード化の必要はないと理解してよいですか？

コメントいただければと思っています。
よろしくお願いします。
No.07900　Re: 一般線形モデルの固定因子について　　【波音】　2008/10/10(Fri) 00:21

>　カテゴリー型の変数を独立変数としたい場合はダミー変数にする必要があると理解していいですか？

そういうことになります。

>　職業を示す変数（1営業，2主婦，3管理職，4事務職）などには順序もないし，間隔もないので，そのまま投入すると変な結果になりますよね？

そ の通りです。SPSSは分かりませんが，どの統計ソフトであっても変数をカテゴリカル型であると指定できる場合が多いので，分析をする前にあらかじめ「こ の変数はカテゴリカル型の変数ですよ」と教えておいてあげる必要があるわけです。そうしないと，連続型の変数として扱われてしまいます。

例えば，Rなんかではas.factor()という関数が使用できるようになっています。

# 職業を表す変数
> job <- c(1, 2, 3, 4, 1, 2, 3, 4)
> job # 中身を表示してみると，これは連続型の変数である
[1] 1 2 3 4 1 2 3 4
> job2 <- as.factor(job) # カテゴリカル型として指定
# 中身を表示すると，4つの水準をもったカテゴリカル型になっている
> job2
[1] 1 2 3 4 1 2 3 4
Levels: 1 2 3 4

>　重回帰やロジスティック回帰の時にはダミーコード化して，一般線形モデルの時にはダミーコード化の必要はないと理解してよいですか？

この辺りを少し誤解されているようです。重回帰分析モデルは独立変数が連続型である場合です。連続型の変数をダミー変数にする必要は全くないわけです。

独立変数がカテゴリカル型の場合は，先ほど説明したように「これはカテゴリカル型だ」とソフトウェアに認識させてあげる必要があります。そうすると，私たちユーザがダミー変数に置き換えなくても，コンピュータ側が勝手に分析してくれるわけです。

ただ，内部的にはカテゴリカル型のデータをダミー変数に置き換えて（すなわち，カテゴリカル型の変数を連続型に置き換えて）分析しているのですね（添付図参照）。

結局，カテゴリカル型の変数を解析する場合，すべてダミー変数に置き換えられているということです。

No.07901　Re: 一般線形モデルの固定因子について　　【ねじきん】　2008/10/10(Fri) 08:38

波音様

丁寧に解説くださってありがとうございます。

>重回帰モデルは独立変数が連続型である場合です。

重回帰は従属変数が連続型で，独立変数に性別（2値の変数）などは投入することがあると思いますが，私の解釈が間違っていますか？
SPSSでは，ロジスティック回帰分析では，独立変数を「この変数はカテゴリー型ですよ」と指定することができるのですが，重回帰や一般線形モデルでは指定が行えません。
た とえば，職業別の血圧（連続変数）に及ぼす影響を重回帰で見たい場合（単純に両者の関係だけを見たい時は，分散分析で行えると思いますが，他に補正したい 変数などがある場合），従属変数を血圧にして，独立変数を職業のダミー変数にして（下記表のように）解析を行うこともあると思っていいですか？
このように職業をダミー変数にしたばあい，コントロールは営業になると思います。
その場合の解釈は，変数1の回帰係数は，「営業に比べて主婦になると血圧がいくつくらい高いか」となると思いますが，考え方が間違っていますか？
同様に，SPSSでは一般線形モデルで「この変数はカテゴリーです」と指定するところがないので，自分でダミー変数を作って，独立変数に投入してもよいでしょうか？

詳しく説明していただいているのに，理解が悪くて申し訳ありません。
教えていただければありがたいです。

表
　　　　変数1　変数2　変数3
1営業　　0　　　0　　　0　　
2主婦　　1　　　0　　　0
3管理職　0　　　1　　　0
4事務職　0　　　0　　　1
No.07904　Re: 一般線形モデルの固定因子について　　【波音】　2008/10/10(Fri) 14:38

>　重回帰は従属変数が連続型で，独立変数に性別（2値の変数）などは投入することがある

一般線形モデルにおいて，独立変数の数と型によっていくつかのモデルが考えられます。それをまとめてみましょう（ちなみに一般線形モデルでは従属変数は連続型に限ります）。

従属変数をY，独立変数をX1， X2とすると，

Y = X1 (X1はカテゴリカル型)　⇒　1要因の分散分析モデル
Y = X1 + X2 + X1*X2（X1，X2は共にカテゴリカル型）　⇒　2要因の分散分析モデル
Y = X1 (X1は連続型)　⇒　単回帰分析モデル
Y = X1 + X2 +　X1*X2（X1，X2は共に連続型）　⇒　重回帰分析モデル
Y = X1 + X2 (X1はカテゴリカル型，X2は連続型)　⇒　共分散分析モデル

といったモデルが代表格です。したがって，独立変数に性別などの変数を投入する場合，それは分散分析モデルになるわけです。もし連続型の変数が混在していれば，それは共分散分析モデルなのです。

>　従属変数を血圧にして，独立変数を職業のダミー変数にして（下記表のように）解析を行うこともあると思っていいですか？

実際に例データで解析してみましょう。

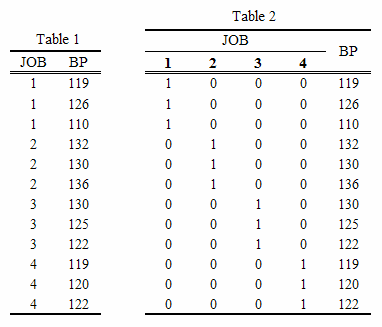
まずJOB（職業）はカテゴリカル型であるので，カテゴリカル型の変数としてコンピュータに認識させて分析します。添付図のTable1のデータのまま解析します。

#　JOBに職業を表すデータを代入する
> JOB <- rep(c(1, 2, 3, 4), c(3, 3, 3, 3))
> JOB <- as.factor(JOB) # カテゴリカル型として指定
> JOB #中身を確認すると，4水準のカテゴリカル型データになっている
 [1] 1 1 1 2 2 2 3 3 3 4 4 4
Levels: 1 2 3 4
# BPに血圧（収縮期血圧）のデータを代入
> BP <- c(119, 126, 110, 132, 130, 136, 130, 125, 122, 119, 120, 122)
> BP # 中身を確認すると，これは連続型である
 [1] 119 126 110 132 130 136 130 125 122 119 120 122
> model <- lm(BP ~ JOB) # 関数lm()を用いてモデル解析
> summary(model2) # 係数表の出力
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  118.333      2.774  42.660 1.01e-10 ***
JOB2          14.333      3.923   3.654  0.00646 ** 
JOB3           7.333      3.923   1.869  0.09850 .  
JOB4           2.000      3.923   0.510  0.62393

続 いて，今度は添付図Table2のデータで分析してみます。これはカテゴリカル型の変数を，自分でダミー変数に置き換えて分析してやるという方法です。 JOB1, JOB2 , JOB3, JOB4は2値データですが，2値データは間隔尺度として扱うことができるので，このように変換して分析することは重回帰分析を行うことと同義なわけで す。

# ダミー変数を用意する。用意するのはJOB1を除いたJOB2-4までの3つでよい。
> JOB2 <- rep(c(0, 1, 0, 0), c(3, 3, 3, 3))
> JOB3 <- rep(c(0, 0, 1, 0), c(3, 3, 3, 3))
> JOB4 <- rep(c(0, 0, 0, 1), c(3, 3, 3, 3))
# JOB2-4の中身を確認。これは全て連続型として扱える。
> JOB2
 [1] 0 0 0 1 1 1 0 0 0 0 0 0
> JOB3
 [1] 0 0 0 0 0 0 1 1 1 0 0 0
> JOB4
 [1] 0 0 0 0 0 0 0 0 0 1 1 1
> model2 <- lm(BP ~ JOB2 + JOB3 + JOB4)
> summary(model2)
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  118.333      2.774  42.660 1.01e-10 ***
JOB2          14.333      3.923   3.654  0.00646 ** 
JOB3           7.333      3.923   1.869  0.09850 .  
JOB4           2.000      3.923   0.510  0.62393

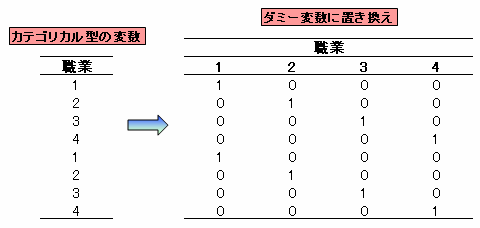
係 数表（Coefficients:の部分）を見ると，どちらも同じ係数が得られていることが確認できるでしょう。先ほどのスレッドでも述べたように，基本 は「カテゴリカル型は全てダミー変数に置き換えられて解析されている」ということで，多くのソフトウェアではそういう手間を省けるように，Rでいうところ のas.factor()という関数があるわけです。

SPSSにそのような機能がなければ，自分でダミー変数を用意して分析するしかないということでもあります。だから，

>　SPSSでは一般線形モデルで「この変数はカテゴリーです」と指定するところがないので，自分でダミー変数を作って，独立変数に投入してもよいでしょうか？

という問いに対しては「その通りです」ということがいえるわけです。

No.07945　Re: 一般線形モデルの固定因子について　　【ねじきん】　2008/10/14(Tue) 16:59

波音様

本当に，本当に詳しく教えてくださってありがとうございます。
内容を読ませていただいて，すっきりしました。
例題のデータをSPSSに入力して確認してみます。

本当にありがとうございます！！

● 「統計学関連なんでもあり」の過去ログ--- 042 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る