「統計学関連なんでもあり」の過去ログ--- 042

No.07720　分散分析の交互作用項について　　【波音】　2008/09/24(Wed) 01:22

解析に使用した変数はBLOOMS（花の数），BED（花壇），WATER（散水量），SHADE（遮光量）の4つです。BLOOMSは連続型，それ以外の3つの変数はいずれもカテゴリカル型の変数です。

まず最初に2つの聞きたいことを挙げさせていただきます。

Q1. 分散分析はダミー変数を用いた回帰分析で同様の結果が得られるが，その場合において交互作用項はどのようにすればよいか。

Q2. Rのlm()関数を使って解析した場合，交互作用項の標準化偏回帰係数をどのように読めばよいか。

まず，lm()を使った2つの方法で交互作用項を含めないモデルを解析してみる。

BED <- as.factor(c(1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2,
	3, 3, 3, 3, 3, 3, 3, 3, 3))
WATER <- as.factor(c(1, 1, 1, 2, 2, 2, 3, 3, 3, 1, 1, 1, 2, 2, 2, 3, 3,
	3, 1, 1, 1, 2, 2, 2, 3, 3, 3))
SHADE <- as.factor(c(1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3,
	1, 2, 3, 1, 2, 3, 1, 2, 3))
BLOOMS <- c(0, 0, 111.04, 183.47, 59.16, 76.75, 224.97, 83.77, 134.95, 
	80.1, 85.95, 19.87, 213.13,
	124.99, 65.48, 361.66, 197.13, 134.93, 10.02, 47.69, 106.75, 246, 135.92, 
	90.66, 304.52, 249.33, 134.59)
# 3つの説明変数はカテゴリカル型であるとして解析
model1 <- lm(BLOOMS ~ BED + WATER + SHADE)
summary(model1)
# ダミー変数で置き換えたデータを用意する（先頭の列を削除した）
BED2 <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0,
	0, 0, 0, 0, 0, 0)
BED3 <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
	1, 1, 1, 1, 1, 1)
WATER2 <- c(0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0,
	1, 1, 1, 0, 0, 0)
WATER3 <- c(0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0,
	0, 0, 0, 1, 1, 1)
SHADE2 <- c(0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0,
	0, 1, 0, 0, 1, 0)
SHADE3 <- c(0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1,
	0, 0, 1, 0, 0, 1)
# これを使って解析
model2 <- lm(BLOOMS ~ BED2 + BED3 + WATER2 + WATER3 + SHADE2 + SHADE3)
summary(model2)

今度は交互作用項を含めたモデルを考えます。

　　　BLOOMS = BED + WATER + SHADE + WATER*SHADE

Rで解析するためには，なんてことはなく同じようにlm()を使って，その際に交互作用項を加えればよいだけですが，，，

model3 <- lm(BLOOMS ~ BED + WATER + SHADE + WATER*SHADE)
summary(model3)

事の発端はmodel3の係数表である，

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)      -1.83      26.93  -0.068 0.946649    
BED2             45.46      19.89   2.286 0.036242 *  
BED3             50.15      19.89   2.522 0.022657 *  
WATER2          184.16      34.45   5.346 6.55e-05 ***
WATER3          267.01      34.45   7.752 8.33e-07 ***
SHADE2           14.51      34.45   0.421 0.679255    
SHADE3           49.18      34.45   1.428 0.172595    
WATER2:SHADE2  -122.02      48.71  -2.505 0.023449 *  
WATER3:SHADE2  -134.81      48.71  -2.767 0.013733 *  
WATER2:SHADE3  -185.75      48.71  -3.813 0.001530 ** 
WATER3:SHADE3  -211.41      48.71  -4.340 0.000507 ***

を解釈しようとしていたことなのですが，最初に示したようにRのlm()関数でも理屈はカテゴリカル変数をダミー変数に置き換えて，先頭の列（WATERという変数ならWATER1）を削除して解析するものだと今まで思っていました。つまり，WATER1を0（基準）としてWATER2とWATER3がどれほどBLOOMSの変動に影響しているかということだと考えていましたが，このような考え方で間違いありませんよね。。。

もし間違いでなければ，交互作用項を含めたモデルを解析する場合でもダミー変数を使って計算できるとはずですが，その場合はどのように（ダミー変数で）表現すれば良いのでしょうか？それともそれは誤りなのか？（これが冒頭にあげたQ1です）

それから，model3の係数表の交互作用の部分の正しい解釈の仕方をもう1度確認したいので教えてください。というか，（ひょっとしたら当たり前すぎることを聞いているのかもしれませんが）交互作用についての係数は本来，WATER1:WATER1, WATER1:WATER2, WATER1:WATER3, WATER2:WATER1, WATER3:WATER1も表示されるべきだと思うのですが，表示されていないということはどういうことでしょうか？これらの値は何処へ？（これがQ2 の詳しい内容です）

ちなみに，使用したデータセットはhttp://www.oup.com/uk/orc/bin/9780199252312/のウェブサイト，[Datasets and supplements] -> [Excel] -> [Datesets one sheet]にあるChapter 07をダウンロードしたものです（Tulipsというシート）。

No.07723　Re: 分散分析の交互作用項について　　【青木繁伸】　2008/09/24(Wed) 11:23

ダミー変数の積で交互作用を表して lm を適用すると，確かに，それ以外の交互作用を加えると，正規方程式が特異行列になりますね。R と同じになるのは，
> summary(lm(BLOOMS ~ BED2+BED3+WATER2+WATER3+SHADE2+SHADE3+
+ I(WATER2*SHADE2)+I(WATER3*SHADE2)+I(WATER2*SHADE3)+I(WATER3*SHADE3)))

Call:
lm(formula = BLOOMS ~ BED + WATER + SHADE + I(WATER2 * SHADE2) + 
    I(WATER3 * SHADE2) + I(WATER2 * SHADE3) + I(WATER3 * SHADE3))

Residuals:
    Min      1Q  Median      3Q     Max 
-72.939 -15.399   1.140  20.666  63.690 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -1.83      26.93  -0.068 0.946649    
BED2                  45.46      19.89   2.286 0.036242 *  
BED3                  50.15      19.89   2.522 0.022657 *  
WATER2               184.16      34.45   5.346 6.55e-05 ***
WATER3               267.01      34.45   7.752 8.33e-07 ***
SHADE2                14.51      34.45   0.421 0.679255    
SHADE3                49.18      34.45   1.428 0.172595    
I(WATER2 * SHADE2)  -122.02      48.71  -2.505 0.023449 *  
I(WATER3 * SHADE2)  -134.81      48.71  -2.767 0.013733 *  
I(WATER2 * SHADE3)  -185.75      48.71  -3.813 0.001530 ** 
I(WATER3 * SHADE3)  -211.41      48.71  -4.340 0.000507 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 42.19 on 16 degrees of freedom
Multiple R-squared: 0.8725,	Adjusted R-squared: 0.7928 
F-statistic: 10.95 on 10 and 16 DF,  p-value: 2.139e-05 
ですね。

たとえば，WATER2, WATER3, WATER1SHADE1, WATER1SHADE2, WATER1SHADE3 は一次従属です。
たとえば，WATER1SHADE3 = 1-WATER2-WATER3-WATER1SHADE1-WATER1SHADE2 となります（これは代入ではなく，等式です）
つまり，
右辺の変数全部0のとき左辺は1
右辺のどれかが1のとき（必ず1変数のみが1になる）左辺は0

No.07732　Re: 分散分析の交互作用項について　　【波音】　2008/09/24(Wed) 18:12

回答ありがとうございます。

とりあえず，どのように指定すればダミー変数を用いた場合でもRと同じ出力結果が得られるのか分かりました。

>　右辺の変数全部0のとき左辺は1
>　右辺のどれかが1のとき（必ず1変数のみが1になる）左辺は0

なるほど，右辺が全部0なら，WATER1SHADE3 = 1-0-0-0-0 = 1で左辺は1，右辺のいずれか1つが1なら，（例えばWATER2が1なら）WATER1SHADE3 = 1-1-0-0-0 = 1-1 = 0で左辺は0となるというわけですね。

ただ，（未だに）イマイチ腑に落ちないというかよくワケが分からないことがあります。ややこしい質問をしてしまいますが，Rでは

model3 <- lm(BLOOMS ~ BED + WATER + SHADE + WATER*SHADE)
summary(model3)

という解析を行うと各要因の最初の水準が基準（0）として計算されますよね（SASやSPSSでは最後の水準が基準とされる）。だから，結局，得られた係数表を式でまとめると添付図の上のような数式が出来上がります。

実はこの交互作用項の"?"が付いている部分（出力されない部分）について混乱しています。

例えば，（Minitabのように）全平均（mean(BLOOMS) = 128.994）を基準にして解析して得られる係数表を式でまとめると添付図の下側の数式のようになります。Minitabでは，実際には各要因の最後の水準が出力されませんが，WATER1 = -77.71, WATER2 = 3.85という数字が得られていれば，これらの値は全平均からの偏差なので（全てを足せば0になるはずなので）-(-77.71)-3.85=73.87 といったように計算できます。

同様の理屈で，交互作用項もWATER1SHADE1(-72.67), WATER1SHADE2(12.94), WATER2SHADE1(29.92), WATER2SHADE2(-6.48)の4つの値が得られれば，求められるでしょう（3*3分割表にしてみると分かりやすい）。
          |           [ W1 ]                           [ W2 ]                          [ W3 ]
-----------------------------------------------------------------
[ S1 ]  |         [ -72.67 ]                       [ 29.92 ]                [-(-72.67)-29.92=42.75]
[ S2 ]  |         [ 12.94  ]                        [ -6.48 ]                [-12.94-(-6.48)=-6.46]
[ S3 ]  | [-(-72.67)-12.94=59.73]    [-29.92-(-6.48)=-23.44]    [-42.75-(-6.46)=-36.29]
--------------------------------------------------------------------
この理屈は理解したのですが，，，「じゃあ，最初の変数を基準にした場合はどうなるの？」という点で混乱しています。
#####     Rで得られた結果からするおと，S1W1とかは？     #####
          | [ W1 ]       [ W2 ]         [ W3 ]
-----------------------------------
[ S1 ]  |  [ ? ]          [ ? ]            [ ? ]
[ S2 ]  |  [ ? ]     [ -122.02 ]     [-134.81]
[ S3 ]  |  [ ? ]     [-185.75]       [-211.41]
-----------------------------------

No.07733　Re: 分散分析の交互作用項について　　【青木繁伸】　2008/09/24(Wed) 19:13

図で添付されている結果ですが，Rの結果はBEDとWATERが入れ替わっています。
それはそれでよいのですが，SHASEではRはレベル1から3で係数が増えるのに，Minitabでは減る方向です。ちょっと変な気がします。
それと，いくつかのレベルの組合せで予測値を計算してみると，RとMinitabでは結果が異なるようなのですけど。。。
Minitabがどのようにしてベースラインに数値を割り付け（他のレベルの数値も再割り付け）しているのか，確認しようにも数値に疑問があると先に進めません。

なお，先に述べた BED, WATER の入れ替えを行ったあと，SHADEも含めた3組の係数について，RとMinitabでの係数の相関をとると，BEDについては1，WATERについては 0.985296979，SHADEについては-0.813291137となりました。SHADEの係数はあきらかにへん。

まあ，係数の下駄履き（下駄脱ぎ？）を適当な基準（たとえば平均や和が0になるなど）で行い，そのしわ寄せを定数項で吸収するということであることは確かなわけだと思います。
そういう観点から言えば，Rの交互作用のところで　？とされているところは 0 だと思います。

No.07734　Re: 分散分析の交互作用項について　　【波音】　2008/09/24(Wed) 21:04

>　図で添付されている結果ですが，Rの結果はBEDとWATERが入れ替わっています。

大変，失礼しました。後でこの記事を参照する人のためにも修正した正しい図を再度，添付しておきます。ちなみに，Minitabの結果についても，交互作用項（WATER*SHADE）において1,1の係数が‐72.72となっていましたが，正しくは‐72.67でしたので，これも加えて修正しておきました。

>　Rはレベル1から3で係数が増えるのに，Minitabでは減る方向です。ちょっと変な気がします。
>　BEDについては1，WATERについては0.985296979，SHADEについては-0.813291137となりました。SHADEの係数はあきらかにへん。

確かに変ですね。しかし，添付図に載せたMinitabの数式は教科書（*1）に載っていた係数表から作ったものでありまして，Minitabを使えない私の環境では追試のしようがありませんね(^_^;)　再度，Rでの解析も確認，教科書の数値も確認したのですがこの通りです。

*1
参考図書　：
　　　野間口・野間口訳「一般線形モデルによる生物科学のための現代統計学」共立出版（2007）　p118

>　そういう観点から言えば，Rの交互作用のところで　？とされているところは 0 だと思います。

なるほど，やはり0となると考えるのが常套ですか。

しかし，，，ホンとになぜSHADEの部分が変なのでしょう。ちなみに，分散分析表はRで行ったものと，教科書（Minitab）で行ったものとピッタリ一致するのですが，これは係数が異なることとは関係のないことなのでしょうか。
# Rで行った場合の分散分析表
# これはMinitabの結果と完全に一致する
            Df Sum Sq Mean Sq F value    Pr(>F)    
BED          2  13811    6906  3.8800  0.042285 *  
WATER        2 103626   51813 29.1116 4.663e-06 ***
SHADE        2  36376   18188 10.2191  0.001382 ** 
WATER:SHADE  4  41058   10265  5.7672  0.004529 ** 
Residuals   16  28477    1780
ちょっと他の例題で比較してみたりしてみます。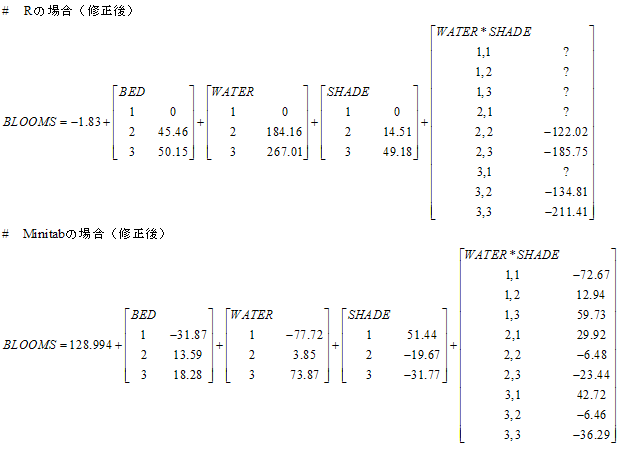

No.07735　Re: 分散分析の交互作用項について　　【知ったかぶり】　2008/09/24(Wed) 22:53

参考になるかどうかわかりませんが，
options(contrasts=c("contr.sum","contr.poly"))
とすると，全平均を切片とする係数値が得られます（そして，その数値は「教科書」のものと完全に一致します）．

No.07736　Re: 分散分析の交互作用項について　　【青木繁伸】　2008/09/24(Wed) 22:59

Good Job!!

今やってみたのですけど，うまくいかない。どこに，options(contrasts=c("contr.sum","contr.poly"))
を入れればよいのでしょうか。。。。

No.07737　Re: 分散分析の交互作用項について　　【青木繁伸】　2008/09/24(Wed) 23:04

ああ，失礼。
最後のカテゴリーをベースラインにするという意味ですね。
確かに，同じ結果になりますね。

No.07738　Re: 分散分析の交互作用項について　　【波音】　2008/09/24(Wed) 23:12

私も一瞬，どこに指定してやればと思ってしまったのですが，実行してみたら同じ結果が得られました。option()で基準にする水準を指定するようなことができたのですね。

No.07740　Re: 分散分析の交互作用項について　　【波音】　2008/09/25(Thu) 00:11

話が一件落着したかのようなトコロで，話題をほじくりかえすようですが，，，

>　最後のカテゴリーをベースラインにするという意味ですね。

これは最後のカテゴリーをベースラインにするという意味なのでしょうか？

例えとしてもっと単純なデータセットを用いて試してみますと。

FERTIL <- as.factor(c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3))
YIELD <- c(6.27, 5.36, 6.39, 4.85, 5.99, 7.14, 5.08, 4.07, 4.35, 4.95, 3.07, 3.29, 4.04, 4.19, 3.41, 3.75, 4.87, 3.94, 6.28, 3.15, 4.04, 3.79, 4.56, 4.55, 4.55, 4.53, 3.53, 3.71, 7.00, 4.61)

# Rの標準時で解析（最初のカテゴリーを基準とする）
result <- lm(YIELD ~ FERTIL)
summary(result)
# 係数表
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.4450 0.3081 17.676 2.28e-16 ***
FERTIL2 -1.4460 0.4357 -3.319 0.00259 **
FERTIL3 -0.9580 0.4357 -2.199 0.03663 *
---

# options(contrasts=c("contr.sum","contr.poly"))を使用
options(contrasts=c("contr.sum","contr.poly"))
result2 <- lm(YIELD ~ FERTIL)
# 係数表
summary(result2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.6437 0.1779 26.109 < 2e-16 ***
FERTIL1 0.8013 0.2515 3.186 0.00363 **
FERTIL2 -0.6447 0.2515 -2.563 0.01627 *
---

一方でSASの場合は次のようになります。
-----------------
Intercept 4.4870
FERTIL1 0.9579
FERTIL2 -0.4880
FERTIL3 0.0000
-----------------

それぞれの方法で得られたモデル式を関数で定義すると，

# Minitabと同じようにした場合
> R.option <- function(FERTIL1, FERTIL2) 4.6437 + 0.8013*FERTIL1 - 0.6447*FERTIL2
# R標準時
> R <- function(FERTIL2, FERTIL3) 5.4450 - 1.4460*FERTIL2 - 0.9580*FERTIL3
# SAS
> SAS <- function(FERTIL1, FERTIL2) 4.4870 + 0.9579*FERTIL1 - 0.4880*FERTIL2
# それぞれのモデル式で群平均を求めてみる。
> F1 <- c(R.option(1,0), R(0,0), SAS(1,0))
> F2 <- c(R.option(0,1), R(1,0), SAS(0,1))
> F3 <- c(R.option(0,0), R(0,1), SAS(0,0))
> my.mat <- rbind(F1, F2, F3)
> colnames(my.mat) <- c("Minitab", "R", "SAS")
> my.mat
Minitab R SAS
F1 5.4450 5.445 5.4449
F2 3.9990 3.999 3.9990
F3 4.6437 4.487 4.4870

としたいところですが，Minitabの場合は全平均をベースラインにしている（？）ので，F3（FERTIL3）の群平均を求める場合は，-0.8013 - (-0.6447) = -0.1566がF3の係数になるので全平均（Intercept）からこの値を引いてあげなければならない。

4.6437 - 0.1566 = 4.4871

と，これで全ての方法でやった結果が一致しますが，これは最後のカテゴリーをベースラインにするというのとはちょっと違うような気がスルのですが・・・

SAS ではまさに最後のカテゴリーをベースラインとしている（FERTIL3の係数は0となっている）といえますが，結局，Rで options(contrasts=c("contr.sum","contr.poly"))を指定する場合やMinitabが採用しているのは「全平均をベースラインにしている」ということなのでしょうか。とすると，ダミー変数のいずれかの列を削除して計算するというのとは，少し違った計算方法をしているということなのでしょうね。

No.07746　Re: 分散分析の交互作用項について　　【知ったかぶり】　2008/09/25(Thu) 09:41

Rは,SASのフリもできるようです．

#Rのデフォルト
R.def<-lm(YIELD~FERTIL)
#Minitabもどき
Minitab<-lm(YIELD~FERTIL,contrasts=list(FERTIL="contr.sum"))
#SASもどき
SAS<-lm(YIELD~FERTIL,contrasts=list(FERTIL="contr.SAS"))

それぞれの計画行列は,
model.matrix(Minitab)
などとすれば表示されますが,Minitabの場合は列和が0となる計画行列であることがわかります．

No.07749　Re: 分散分析の交互作用項について　　【波音】　2008/09/25(Thu) 11:04

ホントですね。実際にやってみるとたしかにSASの結果と一致しますが，こういうやり方ができるとは知りませんでしたから，大変勉強になりました。

しかし，，，こうやってみるとRってスゴイですね(^_^)