No.07610 サンプルサイズが小さい場合の有意差検定 【ATCC】 2008/09/11(Thu) 02:36
生物学の研究に携わっております。統計学にはあまり明るくないので教えていただきたく質問いたします。A群(サンプルサイ
ズ3)B群(サンプルサイズ3)C群(サンプルサイズ3)の3群の間のそれぞれの平均値に有意差があるかどうかを検定したいと考えています。特殊な動物実
験で,入手できる動物材料の数が限られていたためサンプルサイズが小さいのですが,このようなケースで使う事が許される検定方法をご存知のかたがおりまし
たら教えていただきたく思います。t-検定したところp<0.03で有意差ありとなったのですが。
No.07613 Re: サンプルサイズが小さい場合の有意差検定 【青木繁伸】 2008/09/11(Thu) 10:31
並べ替え検定(パーミュテーション・テスト)かな?
これを具体的にやる方法について。
まず,クロス集計表を作ります。測定値をそのまま使って集計表を作ること。g 36.7 45.7 52.4 52.6 61.9 65.3 65.8 76.6 81.3
A 1 0 1 0 0 0 1 0 0
B 0 1 0 0 1 1 0 0 0
C 0 0 0 1 0 0 0 1 1
この集計表について,クラスカル・ウォリス検定の正確検定を行います。URL は
http://aoki2.si.gunma-u.ac.jp/exact/kwtest/getpar.html
実際の実行結果は以下の通り。図をクリックすれば原寸表示。
ちなみに,このデータを一元配置分散分析(等分散を仮定しないウェルチの方法)すると,F = 1.0225, 第1自由度 = 2.000, 第2自由度 = 3.871, P値 = 0.44
となりました。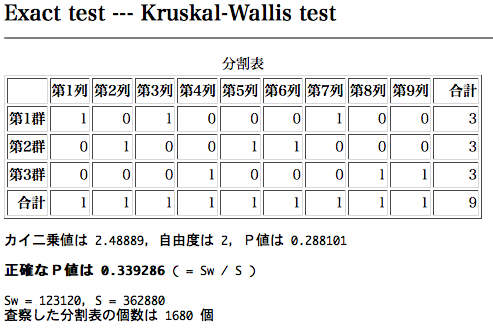
No.07615 Re: サンプルサイズが小さい場合の有意差検定 【ひの】 2008/09/11(Thu) 22:59
クラスカル・ウォリス検定だと,平均値ではなくて中央値の差の検定になりますから質問者の意図と少し違いますね。検出力も落ちます。パーミュテーション法で平均値の差の検定をする手順は,
橘敏明(1997)「確率化テストの方法」日本文化科学社
に書いてあると思います。この本ではパーミュテーション法ではなくてランダマイゼーション法になっていると思いますが,数学的には同じものです(思想的には両者は異なるものらしい)。
No.07617 Re: サンプルサイズが小さい場合の有意差検定 【青木繁伸】 2008/09/12(Fri) 16:05
さて,まず,randomization test と permutation test
の違いは,前者は仮定の範囲内で任意のデータを生成して検定に使うのに対し,後者は標本データの並べ替えで作られるデータを検定に使うところかな?後者で
あっても,n!(すぐに大きくなり,計算不能になる)が大きいときには,n!の並べ替えの中からランダムに抽出して検定に使うしかないので,両者の違いは
少なくなる。
ということで,今回は取りあえず,n が小さいときの permutation test(並べ替え検定)を対象とする。説明のために,3群で,おのおのサンプルサイズが3というデータを考える。
1. 標本データについて3群の平均値の差の検定(一元配置分散分析)を行い P 値を求める。これを P0 としよう。
2. 合計9個のデータを並べる。並べ方は n! 通りあるので,それぞれについて以下を繰り返す。
3. 先頭から3つずつ取って3群の平均値の差の検定(一元配置分散分析)を行い P 値を求める。
4. n! 個の P 値と P0 を比較し,P0 以下の P 値の個数を n! で割ったものが,「並べ替え検定による P 値」である。
なお,P 値によらず検定統計量を使う方法にすることもできる。一般的には検定統計量を使う方が計算量は少ないので好ましいであろう。
これらのことを行う R プログラムは,以下のようになる(非常に簡単に書くことができる)。permutation.oneway.test <- function(x)
{
n <- sapply(x, length)
g <- factor(rep(1:length(x), n))
z <- unlist(x)
library(e1071) # n! 通りの並べ方を求める permutations のあるパッケージ
p0 <- oneway.test(z~g)$p.value # 上記の 1.
perm <- permutations(sum(n)) # 上記の 2.
ps <- apply(perm, 1, function(i) oneway.test(z[i]~g)$p.value) # 上記の 3.
return(mean(ps < p0+1e-10)) # 上記の 4.
}
順列(n!)を求めるプログラムに苦労する事が多かったが,R ではなんと言うことなく使うことができる。9! の全て> head(temp)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 1 2 3 4 5 6 7 8 9
[2,] 2 1 3 4 5 6 7 8 9
[3,] 2 3 1 4 5 6 7 8 9
[4,] 1 3 2 4 5 6 7 8 9
[5,] 3 1 2 4 5 6 7 8 9
[6,] 3 2 1 4 5 6 7 8 9
> tail(temp)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[362875,] 9 8 7 6 5 4 1 2 3
[362876,] 9 8 7 6 5 4 2 1 3
[362877,] 9 8 7 6 5 4 2 3 1
[362878,] 9 8 7 6 5 4 1 3 2
[362879,] 9 8 7 6 5 4 3 1 2
[362880,] 9 8 7 6 5 4 3 2 1
を
計算して,後で使うために変数に代入するのに要する計算時間は,0.25秒(!)である。しかし,それを用いて1組のデータで検定を行うのには17分
(!!)かかる。9! = 362880 であるから,3.での一つの検定はわずか 3
ミリ秒(!!!)で行っているのだけど,これでは,ちょっと実用的ではないし,シミュレーション実験をやるのも容易ではない。
先のやりか
た,プログラムには無駄がある。つまり,各群ごとの3つのデータの順序は,一元配置分散分析では問題にされないが先のプログラムはそれぞれ 6
個の別のデータと見ている。そして,それが 3 群あるのだから
6^3=216回も同じことを繰り返していることになる。これを1回にすれば実行時間は単純に考えれば 1/216 になる。つまり,17
分かかるものが 5 秒で終わることになる。
要するに,順列を考えるのではなく,組合せを考えればよい。AAABBCBCC…のような組合せのリストを求める関数がどこかにあればよいが,これと同じことをやるプログラムが既にある。これを少し改良して,一元配置分散分析に対する並べ替え検定 exact.oneway.testを作った。これによる分析例は以下のようになる。観察値による一元配置分散分析の P 値 = 0.288101
並べ替え検定による P 値 = 0.3392857143
査察した分割表の個数は 1680 個
実行時間はまさに5秒(!)。
「査察した分割表の個数は 1680 個」となっているが,9!/216=1680ということで,出力には現れていないが,「並べ替え検定による P 値」の計算の分母は 9! になっている。
さ
て,用意が調ったので,シミュレーションを行ってみよう。平均値の差の検定を行う一元配置分散分析と比較するのはクラスカル・ウォリス検定とする。上の
permutation.oneway.test 関数や exact.oneway.test 関数の中にある oneway.test
と言うところを kruskal.test に書き換えるだけでよい(使うのは exact.oneway.test)。
3 群,それぞれのサンプルサイズは 3。300組のデータを2つの検定方法で検定し結果を比較する。
シミュレーション 1
3群の母平均は 0, 0.5, 1,母分散は 1。 kruskal.test
oneway.test P>0.05 P<=0.05 Sum
P>0.05 253 12 265
P<=0.05 11 24 35
Sum 264 36 300
所見:どちらの検定も「ダメ」であることに変わりない。そもそも,サンプルサイズが 3 というのはこんなものだ。
シミュレーション 2
3群の母平均は 0, 1, 2,母分散は 1。 kruskal.test
oneway.test P>0.05 P<=0.05 Sum
P>0.05 180 24 204
P<=0.05 17 79 96
Sum 197 103 300
所
見:少しはましになった。でも,検出力は30%そこそこだ。これも甲乙付けがたいが,意外なことに(??)クラスカル・ウォリス検定の方がほんの少し検出
力が高い。(そもそも,並べ替え検定はノンパラメトリック検定であり,「一元配置分散分析で使う検定統計量を使った並べ替え検定は,ノンパラメトリック検
定」なのだ。だから,「クラスカル・ウォリス検定で使う検定統計量を使った並べ替え検定」と比べて,検出力が劣ると言うことはない。いくつか考えられる検
定のどれが優れているかは,どのような検定統計量を使うかである。
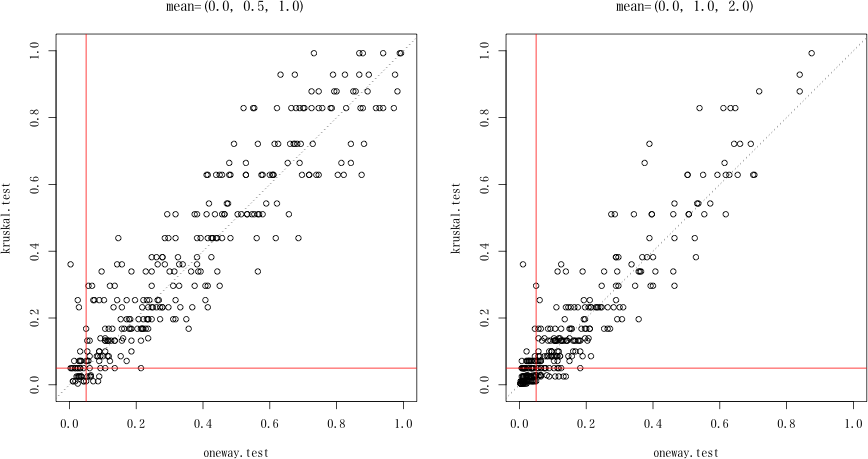
図を描いてみると,以下のようになる。赤い水平・垂直線が
α=0.05 である。波線は傾き 1 の直線である。oneway.test の P 値が kruskal.test のそれよりも小さい(傾き
1 の直線の左にあるものが若干多い)ような気がするが,実際は見た目ほどのこともない。
まとめ
(1) 3群で,各群3例程度のデータではそもそも,あまりたいしたことは言えないようだ
(2) oneway.test, kruskal.test のいずれの検定統計量を使っても,検出力には殆ど違いはない。
図をクリックすると原寸表示
No.07618 Re: サンプルサイズが小さい場合の有意差検定 【青木繁伸】 2008/09/12(Fri) 16:13
シミュレーション実行プログラム(exact.oneway.test 関数のドライバー)set.seed(123)
ans.oneway <- sapply(1:300, function(i)
exact.oneway.test(list(rnorm(3), rnorm(3,1), rnorm(3,2))))
図を描くためのプログラムpdf("fig0912.pdf", width=900/72, height=500/72)
layout(matrix(1:2, 1))
load("ans.oneway")
load("ans.kruskal")
plot(ans.oneway, ans.kruskal, asp=1, xlab="oneway.test", ylab="kruskal.test",
main="mean=(0.0, 0.5, 1.0)", xlim=c(0,1), ylim=c(0,1))
abline(h=0.05, v=0.05, col="red")
abline(a=0, b=1, lty=3)
tbl <- addmargins(xtabs(~I(ans.oneway<=0.05)+I(ans.kruskal<=0.05)))
temp <- dimnames(tbl)
dimnames(tbl) <- list("oneway.test"=temp[[1]], "kruskal.test"=temp[[2]])
tbl
load("ans.oneway2")
load("ans.kruskal2")
plot(ans.oneway, ans.kruskal, asp=1, xlab="oneway.test", ylab="kruskal.test",
main="mean=(0.0, 1.0, 2.0)", xlim=c(0,1), ylim=c(0,1))
abline(h=0.05, v=0.05, col="red")
abline(a=0, b=1, lty=3)
layout(1)
dev.off()
tbl <- addmargins(xtabs(~I(ans.oneway<=0.05)+I(ans.kruskal<=0.05)))
temp <- dimnames(tbl)
dimnames(tbl) <- list("oneway.test"=temp[[1]], "kruskal.test"=temp[[2]])
tbl
No.07619 Re: サンプルサイズが小さい場合の有意差検定 【青木繁伸】 2008/09/12(Fri) 17:57
備忘録として書いておく。
n個の中に,p, q, r,
...個同じものがあるとき(n=p+q+r+…),これらを並べてできる順列のリストは,e1071 の permutations
が速いので,以下のようにしてやれば,一応はできる。ただし,permutations
の戻り値を求める順列に変換することと,重複を除くことに時間がかかるので,ベストではない。comb2 <- function(n.i)
{
n <- sum(n.i)
x <- rep(1:length(n.i), n.i)
library(e1071)
a <- permutations(n)
b <- unique(data.frame(t(apply(a, 1, function(i) x[i]))))
rownames(b) <- 1:nrow(b)
return(b)
}
これを実行すると以下のような結果が得られる。> ans <- comb2(c(3,1,2)) # 順列の個数は (3+1+2)! / 3! / 1! / 2! = 60
> ans
X1 X2 X3 X4 X5 X6
1 1 1 1 2 3 3
2 1 1 2 1 3 3
3 1 2 1 1 3 3
途中省略
57 3 3 1 1 1 2
58 3 3 1 1 2 1
59 3 3 1 2 1 1
60 3 3 2 1 1 1
No.07625 Re: サンプルサイズが小さい場合の有意差検定 【ひの】 2008/09/12(Fri) 22:52
>先のやりかた,プログラムには無駄がある。つまり,各群ごとの3つのデータの順序は,
>一元配置分散分析では問題にされないが先のプログラムはそれぞれ 6 個の別のデータと
>見ている。そして,それが 3 群あるのだから 6^3=216回も同じことを繰り返しているこ
>とになる。これを1回にすれば実行時間は単純に考えれば 1/216 になる。つまり,17 分
>かかるものが 5 秒で終わることになる。
このケースでは3群とも3個ずつなのでこの3群をどの順に並べるかは意味を成さなくなります。具体例で言うと,
A;1, 2, 3
B;4, 5, 6
C;7, 8, 9
と
A;4, 5, 6
B;7, 8, 9
C;1, 2, 3
を区別する必要がない。
したがってさらに3群を並べる順列の数(=3!)で割れます。
9C3 * 6C3 / 3! = 280通り
No.07629 Re: サンプルサイズが小さい場合の有意差検定 【青木繁伸】 2008/09/12(Fri) 23:07
> したがってさらに3群を並べる順列の数(=3!)で割れます。
なるほど。そうですね。
No.07802 Re: サンプルサイズが小さい場合の有意差検定 【ATCC】 2008/10/01(Wed) 10:02
皆様,丁寧に教えていただきありがとうございました。教えていただいた事を参考にして再度検討いたします。
● 「統計学関連なんでもあり」の過去ログ--- 042 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る

