No.05905 Re: 分布の適合 【青木繁伸】 2008/02/18(Mon) 17:06
> マハラノビス距離がどういう分布に従おうが,それと母集団が正規分布に従うのとは何の関係もないでしょう?
と思ったんだけど,やはり,マハラノビス距離を計算するデータは少なくとも多変量正規分布でないとマハラノビスの二乗距離はカイ二乗分布に従わないようですね。# reqire http://aoki2.si.gunma-u.ac.jp/R/mahalanobis.html
sim <- function(p, n=10000, func=rnorm)
{
dat <- data.frame(matrix(func(n*p), n, p))
x <- data.frame(matrix(func(n*p), n, p))
d2 <- Mahalanobis(dat, x)$d2
max.d2 <- 20 # max(d2)
hist(d2, freq=FALSE, main=paste("Mahalanobis's squared distance, population:",
deparse(substitute(func)), ", d.f. =", p),
xlim=c(0, 20), ylim=c(0, 0.2), nclass=20)
x2 <- seq(0, max.d2, length=300)
lines(x2, dchisq(x2, df=p), col="red")
}
set.seed(123)
layout(1:2)
par(cex=1.5)
sim(5, func=rnorm)
sim(5, func=runif)
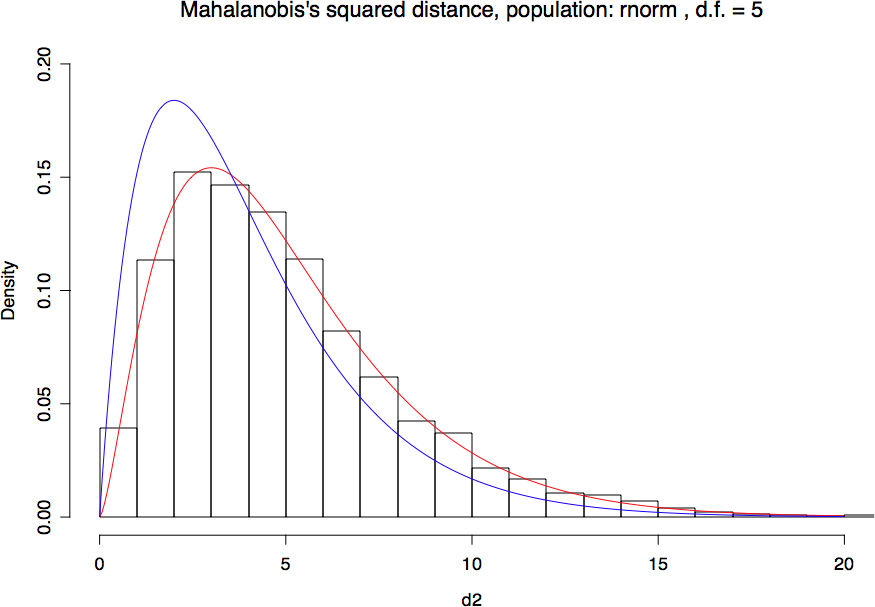
上の図は,5変数の多変量正規分布についてのマハラノビスの二乗距離の分布。赤い曲線はカイ二乗分布(密度関数。自由度は5)。
下の図は,5変数の一様分布について。ヒストグラムと赤い曲線は,ずれている。

No.05967 Re: 分布の適合 【青木繁伸】 2008/02/26(Tue) 23:25
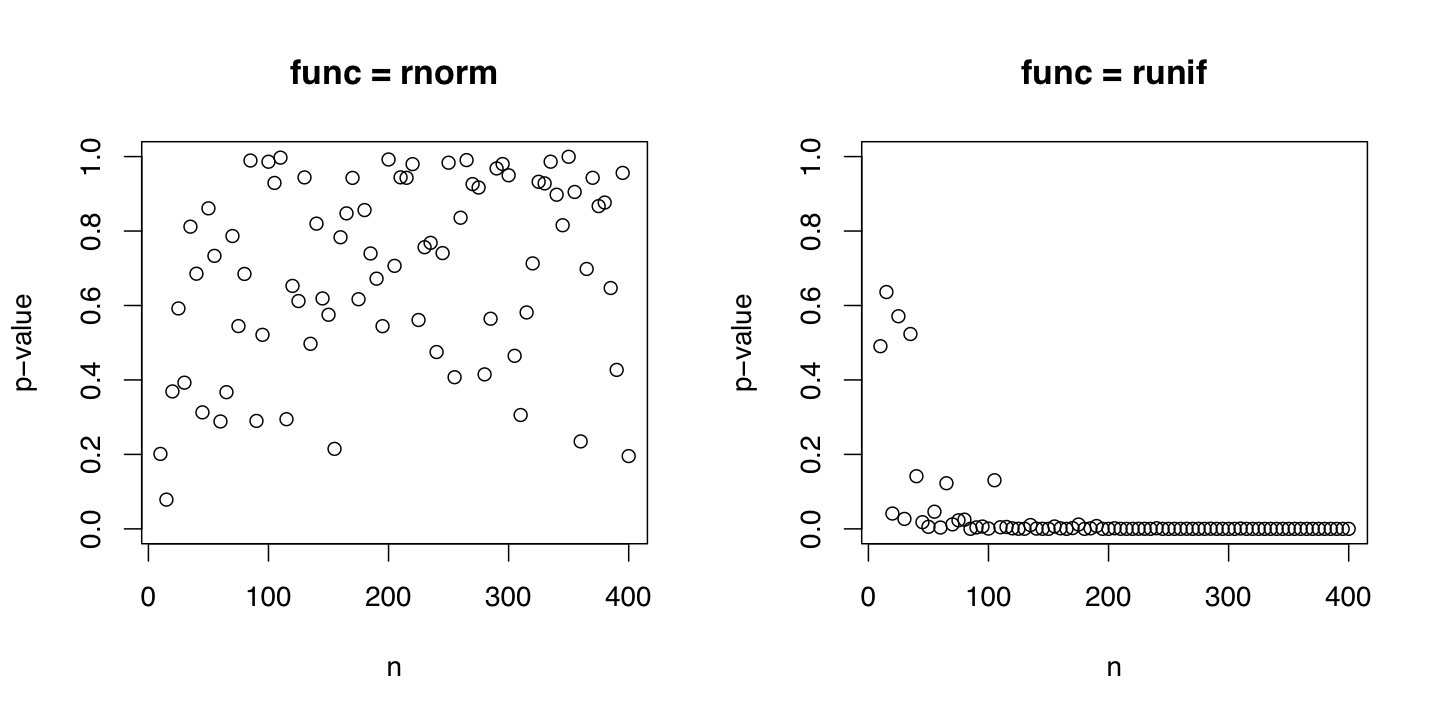
> nが大きくなるほど,p-valueが小さくなった(n = 100, 1000 10000の順にp-value = 0.9862, 0.7363, 0.5013)ので,不思議に思った次第です。
不思議でも何でもないでしょう。
検定では,対象とする統計事象を表す検定統計量の大きさと,サンプルサイズの大きさで有意確率が小さくなるのは,ごくごくごく!当たり前のことです。。。どんな検定でも同じ(検定統計量の算出公式を見れば自明)。
例1 サンプルサイズが10ずつ,対照群での陽性率が40%,処置群での陽性率が60%
例2 サンプルサイズが1000ずつ,対照群での陽性率が40%,処置群での陽性率が60%
(当たり前な注釈:例1も例2も,対照群,処置群での陽性率は同じ!!)
では,検定の実例を> prop.test(c(4,6), c(10, 10))
2-sample test for equality of proportions with continuity correction
データ: c(4, 6) out of c(10, 10)
カイ二乗値 = 0.2, 自由度 = 1, P値 = 0.6547 # ★★★ 有意じゃないよ!!!
対立仮説: 等しくない
95 パーセント信頼区間: -0.7294066 0.3294066
標本推定値:
割合1 割合2
0.4 0.6 # ★★★ ここに注意
> prop.test(c(400,600), c(1000, 1000))
2-sample test for equality of proportions with continuity correction
データ: c(400, 600) out of c(1000, 1000)
カイ二乗値 = 79.202, 自由度 = 1, P値 < 2.2e-16 # ★★★ 有意だよ!!!
対立仮説: 等しくない
95 パーセント信頼区間: -0.2439407 -0.1560593
標本推定値:
割合1 割合2
0.4 0.6 # ★★★ ここに注意 (前と同じでしょ! なんで,いまさら。。。。)