「統計学関連なんでもあり」の過去ログ--- 041

No.05654　仮説検定　　【マーシャル】　2008/02/01(Fri) 16:32

仮説検定に関する質問です。
P値というのがありますが，仮説の採択・不採択より進んだ判定をするために使う指標と文献を見ると書かれていますが，標準正規分布に近似をしてZの値を求めていく所までは理解しました。しかし，そこから検定のP値を求めていくというところが理解できません。その点に関してお願いします。

No.05655　Re: 仮説検定　　【青木繁伸】　2008/02/01(Fri) 18:06

Z と P の関係は図のようになります。赤の斜線で囲んだ部分の面積が，「Z より大きい値，及び -Z より小さな値を取る確率」で，これが P 値です。
統計学の教科書の後ろの方に標準正規分布表等というのがあれば，ZからPを読み取ることができます。
正確な値を求めるにはコンピュータが必要です。
たとえばエクセルなら，Z=1.5 ならば，セルに =(1-NORMSDIST(1.5))*2 と入力すると 0.133614403 が得られます。
R なら，pnorm(1.5, lower.tail=FALSE)*2 とすればよいですね。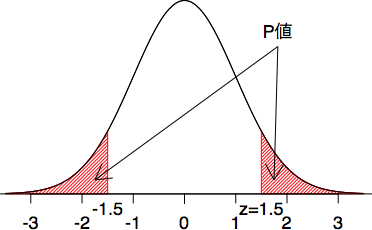

No.05659　Re: 仮説検定　　【マーシャル】　2008/02/01(Fri) 18:50

説明ありがとうございます。仕組みはわかりましたが，標準正規分布表でZからPを読み取ることが出来ません。どこに注目すればいいのでしょうか？
お願いします。

No.05668　Re: 仮説検定　　【青木繁伸】　2008/02/01(Fri) 21:14

> 標準正規分布表でZからPを読み取ることが出来ません

その教科書に説明がないのですか？　欠陥教科書ですね
添付する標準正規分布表は，標準正規得点がz以上になる確率を記載しています。
表の左端の列は標準正規得点の小数点以下1桁までの数値を表しています。小数点以下2桁目の数値は各列に対応しています。Z=1.5の時の数値は左端に 1.5と書かれている行（赤枠で示しました）の一番上の行に0.00 と書かれた列（これも赤枠で表示）つまり実際のZが1.5+0.00=1.50 に対応するのは枠の交差する枠内にある数値 0.0668 ということです。この数値は，先に示した図で言えば右側にある赤い斜線で引いた部分の確率ですので，左側の部分の確率も加えないといけません。左右対称なので，今求めた 0.0668 を2倍すればよいということです。つまり 0.0668×2 = 0.1336 ということです。

教科書のどこかに書いてあることだと思いますよ

図をクリックすれば，原寸大で表示します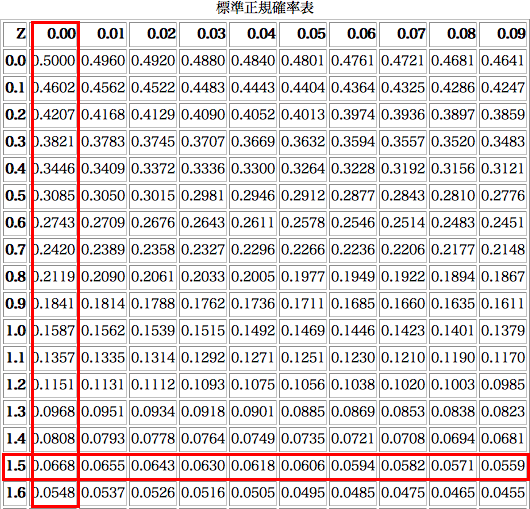

No.05676　Re: 仮説検定　　【マーシャル】　2008/02/02(Sat) 01:18

ようやく求め方のプロセスが見えてきました。
確率と正規分布表では関連性があるのかと，思い込んでいました。
再度別な教科書を探して繰り返し復習します。
丁寧な説明ありがとうございます。