No.05457　ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/21(Mon) 14:46

　はじめて質問させていただきます。
　投稿中の論文の統計について，レフェリーからクレームを受けて困っております。下記の統計解析の手法が妥当かどうか，ご意見をいただけないでしょうか。

　 あるノックアウトマウスの野生型と変異体との行動を比較する目的で，仔マウスに対する行動（かわいがる，いじめる，いずれでもない）の3種類をとる率を， 4種類の実験条件において，行動観察により調べました。データとしては，2x3のクロス集計表が4つ分になります。添付書類に集計した棒グラフを示してお ります。

　初回投稿時にはFisher exact test（2x3）により，それぞれの実験条件で野生型と変異体が異なるということを示しておりました。
　ところが，これではどの行動が変異体で増えたり減ったりしているのかがわかりにくいというレフェリーのコメントを受け（グラフから明らかだと思うのですが・・）仕方なく，
かわいがる＝（1,0,0）
いじめる＝（0,1,0）
いずれでもない＝（0,0,1）
とダミー変数に変換してSPSSで二元配置分散分析を行いました。

　すると，このような統計手法が妥当かどうか，統計専門家に確認しなさいというレフェリーの再コメントを受けました。

　 なお，ダミーデータに変換する際，いずれかに分類されるはずの3つの行動様式をそれぞれ独立としましたので冗長になっておりますが，通例省かれる「どちら でもない」を省いてしまうと，変異体では「どちらでもない」が野生型に比べ常に増えている（グラフの黒い部分）というもっとも明らかな観察結果が統計上わ かりにくくなってしまいますので，このようにいたしました。

このままいければうれしいのですが，これで妥当でしょうか？
何卒よろしくお願いいたします。

No.05458　追記: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/21(Mon) 16:02

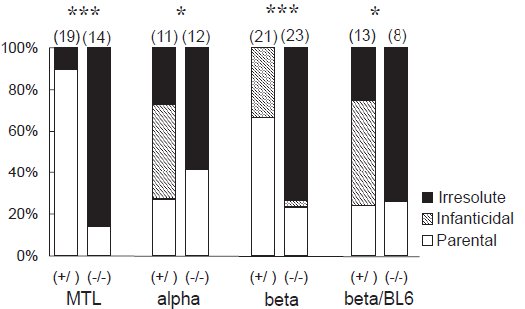
上記記事のデータです。
genotype condition    Behavior No of mice
      WT        10    parental         17
      WT        10 infanticide          0
      WT        10  irresolute          2
      WT        20    parental          3
      WT        20 infanticide          5
      WT        20  irresolute          3
      WT        30    parental         13
      WT        30 infanticide          0
      WT        30  irresolute          9
      WT        40    parental          3
      WT        40 infanticide          7
      WT        40  irresolute          3
      KO        10    parental          2
      KO        10 infanticide          0
      KO        10  irresolute         12
      KO        20    parental          5
      KO        20 infanticide          0
      KO        20  irresolute          7
      KO        30    parental          6
      KO        30 infanticide          1
      KO        30  irresolute         16
      KO        40    parental          2
      KO        40 infanticide          0
      KO        40  irresolute          6
No.05459　Re: ダミー変数を用いた二元配置分散分析　　【青木繁伸】　2008/01/21(Mon) 17:08

このデータをどうやって二元配置分散分析したのでしょう？
No.05460　Re: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/21(Mon) 17:46

お返事ありがとうございます。具体的には，上記データを次のようにダミー変数に変換しました。
Genotype	cond　parental	inf	irresolute
0 	10 	1 	0 	0 
0 	10 	1 	0 	0 
0 	10 	1 	0 	0 

途中省略

1 	40 	1 	0 	0 
1 	40 	1 	0 	0 
1 	40 	0 	0 	1 
1 	40 	0 	0 	1 
1 	40 	0 	0 	1 
1 	40 	0 	0 	1 
1 	40 	0 	0 	1 
1 	40 	0 	0 	1
それから，SPSSの一般線形モデル→多変量とし，ConditionとGenotypeを固定因子，Par, Inf, Irrを
従属変数としました。
（さらに「その後の検定」にとりあえずTukeyを選択しましたが，これは不適切かもしれません。）

　何卒よろしくお願いいたします。

(段落中でリターンキーを押して一行の文字数を調整しないでください）
No.05513　Re: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/24(Thu) 15:30

この掲示板の5481-82での議論を拝見したのですが，

＞二値変数は名義尺度であると同時に間隔尺度としても扱えるのです。
3 つ以上のカテゴリーを含む名義尺度（順序尺度）変数は，カテゴリー数より一つだけ少ない複数のダミー変数に変換して多変量解析に利用できます。多くの統計 解析パッケージでは，カテゴリー変数であることを宣言しておけば重回帰分析などに使ったときに自動的にダミー変数に展開してちゃんと分析してくれます。

　ということでしたら，私どもの問題も，ダミー変数にして多変量解析しても問題ないのかと思うのですが，いかがでしょう？冗長性が残っていることが問題なのでしょうか。

　仮に，30分の行動観察中，（養育parental，いずれでもないneither　喰殺infanticide)のいずれかの行動をとっていた時間を計測していたならば，上のデータが
0-1ではなく0分から30分以内の連続的な値をとることになり，この場合ならばANOVAで処理してもとくにクレームはつかないと思います。
　 しかし，実際のマウスの行動としては，3つのうちのいずれかになります。つまり，30分のうち，喰殺したり養育したりするということは現実にはなく，マウ スはほとんどの時間を養育しているか，あるいは一人で寝ているか，あるいはさっさと喰殺してしまうかという，3方向に極端な行動をとります。それで簡単の ためにカテゴリーとしてデータをとった次第です。
ですので，このように変換してANOVAをするのは，実験者としてはごく自然な感じがするのですが・・

　多変量解析の結果はグラフから直感的にわかることとよく一致していましたし，これでどうしていけないのかがわからないのですが・・
　ご教授いただければ幸いです。
No.05537　Re: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/25(Fri) 19:34

度々申し訳ありませんが，投稿中の論文であり，この1ヶ月ほど，この問題でほんとうに困窮しております。
お忙しいところ恐縮ですが，「はっきりとはいえないが，〜だと思う」「この先生に相談すればわかるかもしれない」など，どんなご意見でも結構ですので，何卒宜しくお願い申し上げます。
No.05540　Re: ダミー変数を用いた二元配置分散分析　　【青木繁伸】　2008/01/25(Fri) 21:19

回答がない理由というのは幾つも考えられます（おわかりかと思いますが）

質問を見たけど，読み流した
質問を見たけど，さっぱり分からない
回答することはできるが，答える暇がない
回答できるけど，いろいろな意味で，回答する必要性を見いだせない
回答するにはもう少し情報が必要だ
潜在的な回答者が，この質問をまだ見ていない
そもそも，この掲示板を見ているもののうちに回答できるものがいない

専門の統計アドバイザに当たってみるのがよろしいかも
No.05541　Re: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/01/26(Sat) 11:38

青木先生
お返事ありがとうございます。おっしゃるとおりだと思います。
すでに国内3社，海外2社の統計コンサルタント会社に相談していますが結論を得ていません。
もし，「専門の統計アドバイザ」の先生を具体的にご存知でしたら，ご示唆いただけないでしょうか。ご面倒でしたら無視していただいてかまいませんし，その場合は以降お騒がせいたしません。

何卒よろしくお願いいたします。
No.05909　Re: ダミー変数を用いた二元配置分散分析　　【Kuroda】　2008/02/19(Tue) 16:52

その後，やはり分散分析は不適切ではないかということで，いろいろ試行錯誤したのですが，ダミー変数を用いないで そのまま3水準の応答としてRのmultinomにより解析できました。ダミー変数に変換してglmを用いてもほぼ同じように解析することができました。 ありがとうございました。
No.05911　Re: ダミー変数を用いた二元配置分散分析　　【ごう】　2008/02/20(Wed) 07:17

〜だと思うとか〜の気がすると言う程度のお話ですが。
こちらも素人ですので。
まず，従属変数を多項分布に従うという前提かなあと。
で，もしこれが面倒であるなら，マウスの行動を正常と異常（食べちゃう）の2種類に分けてfisher.testするとか，glm(family=binomial)してしまうとか。

2*3の分割表のままfisher.testしたいなら
10　20　30
30　20　10
みたいな表の場合
10　20
30　20
でfisher
20 30
20 10
でfisher
10 30
30 10
でfisher
と総当たりさせた上でBonferroniなり改良Bonferroniaあたりで多重比較するとかはどうなんでしょう？
間違っていたら，誰かがその旨指摘してくれることを期待して記載してみました。
No.05912　Re: ダミー変数を用いた二元配置分散分析　　【ごう】　2008/02/20(Wed) 07:25

書き忘れ。
あと，Breslow-Day 検定とかMantel-Haenszelあたりの組み合わせになりそうな「気がします」
No.05913　Re: ダミー変数を用いた二元配置分散分析　　【TY】　2008/02/20(Wed) 09:37

multinomial logit modelで検索したらこのようなものが見つかりました。本文中の使用ソフトはSASですが，参考までに。
http://support.sas.com/techsup/technote/ts722g.pdf
Wikipediaも参考までに。
http://en.wikipedia.org/wiki/Multinomial_logit
generalized logits modelについて追記
http://support.sas.com/onlinedoc/913/getDoc/ja/statug.hlp/catmod_sect9.htm
http://support.sas.com/onlinedoc/913/getDoc/ja/statug.hlp/logistic_sect57.htm
SPSSの情報追加
http://www.spss.co.jp/labo/ttips/03/
No.05914　Re: ダミー変数を用いた二元配置分散分析　　【kai】　2008/02/20(Wed) 16:50

SASかJMPを使用すれば多変量ロジスティック回帰分析で解析可能だと思いますが，SPSSやRは使った事がないのでわかりません．
JMPで解析したところ交互作用とGenotypeの主効果が有意有りという結果になりました
No.05915　Re: ダミー変数を用いた二元配置分散分析　　【青木繁伸】　2008/02/20(Wed) 17:03

multinomial ですから，多変量ロジスティックではなく，多項ロジスティックでしょう？
多変量ロジスティックは，従属変数が2値データ。独立変数は多変量。
多項ロジスティックは，従属変数が2値より多くの値を取る。独立変数は多変量。
R での多項ロジスティックは
http://news.fbc.keio.ac.jp/~hamaoka/YuhikakuR-chap8/index.html
等も参考になるかも。
No.05921　Re: ダミー変数を用いた二元配置分散分析　　【kai】　2008/02/21(Thu) 08:22

>multinomial ですから，多変量ロジスティックではなく，多項ロジスティックでしょう？

そうですね．済みません
JMPでは名義ロジスティックという名前になってました．
（JMPやSASでは従属変数が2値かそれ以上かで区別はされていません）

● 「統計学関連なんでもあり」の過去ログ--- 041 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る