「統計学関連なんでもあり」の過去ログ--- 041

No.05197　多重比較について　　【こまった】　2007/12/28(Fri) 05:20

以前質問させて頂きましたが，もう一度お願いいたします。（過去ログ4752）

以前，対応のあるデータと対応のないデータについて青木先生にご指導頂きありがとうございました。
まず，再度私が行っている実験についての説明ですが，研究の概要としては養護小学校で7人の生徒を対象に，家具のレイアウトの変更前（6日間）と変更後（6 日間）に活動内容がどのように変化するかを調べるといったものです。方法は，30分ごとに所定の用紙に活動行為（会話・勉強等）を書きこんでいくというプロット調査行いました。

そして添付したファイルのように一つの活動項目に着目し，レイアウト変更前と変更後に差があったのかどうかの有意性を調べるといったものです。
このデータについては以前ご指導頂いたき対応がないデータであると理解し，マンホイットニーのU検定を用い，検証していきました。

先日，別の養護学校で同じ実験を行ったのですが，今回はレイアウト変更後4日目にさらにもう一度レイアウトを変更するといった手順を加えました。そのデータ例についても添付しています。
私の担当教官に，日常，変更後，再変更後は対応のないデータだからクラスカルウォリスの検定を用いて分析しなさいとメモ書きを残し，教官はそのまま休暇に入ってしまいました。私は，日常データは時系列にならべただけのデータであって変更後，再変更後と対応がないと思うのですが，変更後，再変更後のデータについては，時系列が意味を持つため，対応のあるデータではないかと考えいるのですが，どうなんでしょうか？。担当教官と連絡が取れないため，再度お邪魔させていただきました。

このように，対応のないデータと対応のあるデータが組み合わさっている場合，日常と変更後，日常と再変更後の2組の組み合わせをつくり，分析するものなのでしょうか？また，シェッフェかスティールドュワスかスティールの多重比較を用いて分析していこうと考えているのですが，これらの分析はクラスカル・ウォリスの後に用いている事例が多いのですが，単体で用いることはできるのでしょうか？

御多忙の所，長々と申し訳ございませんが，どうぞよろしくお願いします。

No.05202　Re: 多重比較について　　【知ったかぶり】　2007/12/29(Sat) 11:44

以前の青木先生とのやり取りを読んでいて気になったことをいくつか（解答ではありませんが）．

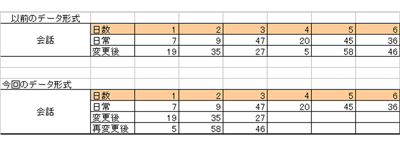
＞今回の実験期間は計2週間で，レイアウト変更前を月～土の1週間（日曜日は休み），そして次の週の月～土の1週間をレイアウトを変更して調査を行いました。そのため，学校で行われるプログラム（授業の内容や休み時間）がレイアウト変更前と後で同一なのでデータの元が同じであり，「対応がある」と判断しました。

活動内容がプログラム（授業の内容や休み時間）によって影響を受けるのであれば，これは対応のあるデータと考えるべきです．曜日によって条件が異なるわけですから，観測結果は曜日毎に対にする必要があります．

＞日常データは時系列にならべただけのデータであって変更後，再変更後と対応がないと思うのですが，変更後，再変更後のデータについては，時系列が意味を持つため，対応のあるデータではないか

？？？　これは何か勘違いをされているのだと思います．

＞正規性の検定を行った所，正規性はなかった

適合度の検定を行ったのだと思いますが，サンプルサイズが6と小さいので，かなり極端な場合を除いて，帰無仮説が採択される，すなわち「正規分布でないとは言えない」という結果になると思います（少なくとも例として示されたデータでは，そうなります）．だからといって正規分布を仮定してよいとは限りませんが．．．

＞30分ごとに所定の用紙に活動行為（会話・勉強等）を書きこんでいくというプロット調査

観測時点の各人の活動が調査項目のどれか一つに必ず入る（一つだけ入る）ということでしょうか？また，もしかして曜日によって観測回数に差があるのではありませんか？そうであれば，比率のデータとして扱った方がよいように思います．

No.05207　Re: 多重比較について　　【こまった】　2007/12/29(Sat) 21:55

お返事ありがとうございます。

＞活動内容がプログラム（授業の内容や休み時間）によって影響を受けるのであれば，これは対応のあるデータと考えるべきです．曜日によって条件が異なるわけですから，観測結果は曜日毎に対にする必要があります．

先日実験を行った学校では一応曜日ごとにプログラムが決まっているのですが，養護学校ということもあり，その日通りのプログラムが確実に行われているわけではありませんでした。ですから，対応のないデータとして扱おうと考えました。

＞適合度の検定を行ったのだと思いますが，サンプルサイズが6と小さいので，かなり極端な場合を除いて，帰無仮説が採択される，すなわち「正規分布でないとは言えない」という結果になると思います（少なくとも例として示されたデータでは，そうなります）．だからといって正規分布を仮定してよいとは限りませんが．．．

おっしゃる通りです。私の書き方が間違ってました。サンプルサイズが小さいので「正規分布でないとはいえない」とい結果です。確実に正規分布とはいえないので，ノンパラを用いようと考えたのですが，この場合，パラメトリックな方法とノンパラは方法ではどっちを用いる方が有用なのでしょうか？教えてください。

＞観測時点の各人の活動が調査項目のどれか一つに必ず入る（一つだけ入る）ということでしょうか？また，もしかして曜日によって観測回数に差があるのではありませんか？そうであれば，比率のデータとして扱った方がよいように思います．

はい。各人の活動が調査項目のいずれかに当てはまります。どの曜日も朝9時～夕方3時までの計6時間調査を行ったため，観測回数に差はありません。説明不足で申し訳ありません。

No.05218　Re: 多重比較について　　【知ったかぶり】　2007/12/30(Sun) 15:53

＞この場合，パラメトリックな方法とノンパラは方法ではどっちを用いる方が有用なのでしょうか？

上限のあるカウントデータで，サンプルサイズも小さいので，正規性を仮定するのはムリがあると思います．ノンパラメトリックな手法を適用するのが妥当ではないでしょうか．

＞日常と変更後，日常と再変更後の2組の組み合わせをつくり，分析するものなのでしょうか？また，シェッフェかスティールドュワスかスティールの多重比較を用いて分析していこうと考えているのですが，これらの分析はクラスカル・ウォリスの後に用いている事例が多いのですが，単体で用いることはできるのでしょうか？

実験の目的がわからないので，ハッキリしたことは言えませんが，コントロール（日常）とそれぞれの処理（変更後，再変更後）の比較だけを行うのであれば，検定を繰り返しても多重検定とならない場合もあります．「多重性」などのキーワードで，過去ログを検索することをお勧めします．

多重比較の前に分散分析が必要か，という質問はこれまでも何度か出てきていますが，必要ないというか，やるべきではないという考え方が主流のようです．ノンパラの場合も同様に考えてよいと思いますが，その辺は分野によっても異なりますので，先行研究に習った方が無難だと思います．

たぶん，一番の問題は再変更後のデータが「独立ではない」ことだと思います．対処法としては．．．「1回目の変更は，再変更後の各人の活動に影響を与えてはいない」と仮定するしかないのでは．．．

いらんお節介かもしれませんが，この実験では個人が識別されている，つまり7人一人一人についてデータが揃っているのではありませんか．のべ人数としてまとめてしまうと情報を捨てることになり，もったいない様な気がします．

No.05268　Re: 多重比較について　　【こまった】　2008/01/06(Sun) 03:33

お返事を頂いたにも関わらず，返信遅くなり申し訳ありません。

＞実験の目的がわからないので，ハッキリしたことは言えませんが，コントロール（日常）とそれぞれの処理（変更後，再変更後）の比較だけを行うのであれば，検定を繰り返しても多重検定とならない場合もあります．「多重性」などのキーワードで，過去ログを検索することをお勧めします．

すみません，過去ログを探したのですが見つけることができなかったので，もう一度だけ教えてください。実験の目的としては，日常と変更後，再変更後を比較して行為の活性化が見られるかどうかといったこです。また，それがどのような活動内容であったかを把握していくことを目的としています。
そこで質問ですが，「日常と変更後」，「日常と再変更後」の2組でそれぞれマン・ホイットニーのU検定で検定を行うということは有用な方法なのでしょうか？教えてください。

＞7人一人一人についてデータが揃っているのではありませんか．のべ人数としてまとめてしまうと情報を捨てることになり，もったいない様な気がします．

アドバイスありがとうございます。その点も考慮しながらもう一度分析方法考え直したいと思います。

お忙しい所，何度も質問して申し訳ありません。どうぞよろしくお願いします。

No.05273　Re: 多重比較について　　【知ったかぶり】　2008/01/07(Mon) 13:54

＞「日常と変更後」，「日常と再変更後」の2組でそれぞれマン・ホイットニーのU検定で検定を行うということは有用な方法なのでしょうか？

全体としての帰無仮説が「レイアウト変更により活動内容に違いは生じなかった」であれば，検定を繰り返すことにより（全体としての）有意水準が低下します。したがって，多重比較により有意水準を調整する必要があります。
レイアウト変更によって活動内容が変わることが「わかって」いて，特定の変更方法について個々に検討するだけであれば，検定を繰り返しても多重性は問題とはなりません。

No.05295　Re: 多重比較について　　【こまった】　2008/01/08(Tue) 22:03

検定を繰り返す場合は，ボンフェローニ等で有意水準を調整すればいいわけですね。

いろいろとご教授頂きありがとうございました。