「統計学関連なんでもあり」の過去ログ--- 041

No.05109　y切片0での単回帰の時のR^2の意味　　【小野寺】　2007/12/17(Mon) 10:04

y切片をゼロに固定して回帰直線を引いたときのR^2は，y切片を固定しなかった時のR^2と比較できない理由が分かりません。
このことについて，
http://aoki2.si.gunma-u.ac.jp/Hanasi/StatTalk/11.html
でお話があり，スネデッカー・コクラン著（畑村，奥野，津村訳）「統計的方法原書第6版」に詳しく書いてあるとのことです。
しかし，古い本のうえ安くはないようでしたので，詳しい説明のある新しい本があれば
教えて頂けないでしょうか。

もしくは，簡単な理由であれば教えて頂けないでしょうか。

No.05110　Re: y切片0での単回帰の時のR^2の意味　　【青木繁伸】　2007/12/17(Mon) 10:21

定義が異なるから比較できないだけです

また，もしデータが第一象現に分布していて相関が負のとき，だれも原点を通る回帰直線を当てはめようとはしないだろうということもありますが。

なお，スネデッカー・コクランには，原点を通るときのR^2の求め方について詳しく書いてあるのです（といっても，そのページの下の方に書いてあることとおなじですが）。

No.05113　Re: y切片0での単回帰の時のR^2の意味　　【小野寺】　2007/12/17(Mon) 14:48

ご回答，どうもありがとうございます。
「R^2 = 予測値の平方和/ yの平方和」の平方和を偏差平方和と間違え，通常のR^2と何が違うのか？と勘違いしておりました。
なぜ，y切片を0に固定するとR^2の計算方法を変える必要があるのでしょうか。また，かなり予測値がばらついていても高い値がでるようですが，そのR^2 はどのように解釈すればよいのでしょうか。このあたりの事がスネデッカー・コクランなどに書いていないかと期待していたのですが・・・。

No.05114　Re: y切片0での単回帰の時のR^2の意味　　【青木繁伸】　2007/12/17(Mon) 14:53

> y切片を0に固定するとR^2の計算方法を変える必要があるのでしょうか

同じやり方でやると，Excel のように，R2 が負になったりして，かな～～り，みっともないことになるわけです。（というか，そのような場合には別の定義式があるということだけなんですが，Excel はそれを知らないだけ）

> かなり予測値がばらついていても高い値がでるようですが

具体例を示してみてください。

No.05119　Re: y切片0での単回帰の時のR^2の意味　　【小野寺】　2007/12/17(Mon) 16:44

ご回答，どうもありがとうございます。
それでは，具体例を示させて頂きます。
x　　　y
3.7　　5
6.2　　9
4.0　　4
3.3　　3
2.5　　1
6.5　　7
4.5　　7
3.3　　5
3.3　　1
6.3　　6
3.0　　4
2.4　　2
2.7　　1
4.8　　8
5.1　　3
2.9　　3
5.2　　5
6.4　　8
3.2　　4
3.3　　6
回帰式はy切片を0に固定して　y= 1.1353x
「R^2 = 予測値の平方和/ yの平方和」では　R^2=　0.9087
「R^2 = 予測値の分散/ yの分散」では　R^2=　0.4198　でした。
この場合，後者のR^2を計算するのは無意味なのでしょうか。また，前者のR^2はどのように解釈されるのでしょうか。
お手数をおかけしますが，よろしくお願いします。

No.05123　Re: y切片0での単回帰の時のR^2の意味　　【青木繁伸】　2007/12/17(Mon) 18:03

> 「R^2 = 予測値の平方和/ yの平方和」では　R^2=　0.9087
> 「R^2 = 予測値の分散/ yの分散」では　R^2=　0.4198　でした。
> この場合，後者のR^2を計算するのは無意味なのでしょうか。

無意味でしょう。
原点を通ると言うことは原点周りのモーメントを考えることになります
原点周りの平方和は Σ(測定値-0)^2= Σ測定値^2
原点を通らない普通の回帰直線は「平均値を通る」わけですから，平均値周りの平方和は Σ(測定値-平均値)^2=変動です。変動をn-1で割ったら不偏分散です。

予測値の分散/ yの分散　というのは，原点を通るといっていながら平均値周りの平方和（変動）を使っているから変なんです。

> 前者のR^2はどのように解釈されるのでしょうか

文字通り，yの予測値の平方和とyの平方和の比ですが。

平均値周りの平方和の比と原点周りの平方和の比の比較は不可能です。よね。

No.05138　Re: y切片0での単回帰の時のR^2の意味　　【小野寺】　2007/12/18(Tue) 19:47

ご回答，ありがとうございました。
y切片を0に固定した場合，「R^2 = 予測値の分散/ yの分散」が不適当である事が分かりました。
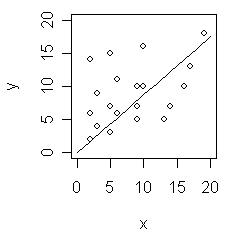
y 切片を0に固定しない場合，「yの分散= 予測値の分散+ 残差の分散」なので，R^2は回帰式がyの動きをどれだけ説明できているかの割合を数値でそのまま表しており，目安ですが0.8以上でよい精度という尺度が書いてある本もあります。y切片を0に固定した場合のR^2からも，こうした何かの意味を読めるのでしょうか。それとも，ただ数値が高い方がよく説明している回帰式であるというだけなのでしょうか。例えば，下図の架空データではR^2=0.7344 であり，いろいろな架空データで試すと全体的に高い値と思います。目安の尺度はあるでしょうか。