「統計学関連なんでもあり」の過去ログ--- 041

No.04694　非線形回帰曲線について　　【ぼのぼの】　2007/11/13(Tue) 02:54

非線形回帰曲線について困っています。
曲線のタイプとしては線形-2次モデルで
y=EXP(-ax-bx^2)
です。SPSS，Rなどを用いて回帰させようとしているのですが，どうしても一定の値に収束しません。
x y
0 1
2 0.81
4 0.28
6 0.10
8 0.02
データの個数が少ないのが原因でしょうか。
どうぞよろしくおねがいします。

No.04695　Re: 非線形回帰曲線について　　【青木繁伸】　2007/11/13(Tue) 08:11

データが少ないから一定の値に収束しないのではないでしょう。
初期値の探索をするには，Excelでグラフを描いて対話的にやるというのも良いかと。

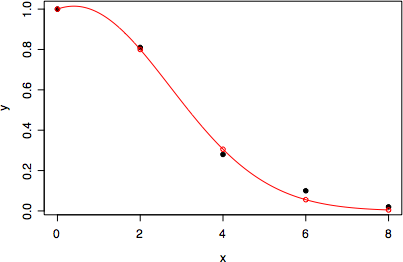
> x <- 0:4*2
> y <- c(1,0.81,0.28,0.10,0.02)
> ans <- nls(y~exp(-a*x-b*x^2), start=list(a=0.4, b=0))
> summary(ans)

Formula: y ~ exp(-a * x - b * x^2)

Parameters:
  Estimate Std. Error t value Pr(>|t|)   
a -0.07320    0.04256  -1.720  0.18393   
b  0.09238    0.01404   6.579  0.00715 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 0.03132 on 3 degrees of freedom

Number of iterations to convergence: 8 
Achieved convergence tolerance: 7.111e-06 

> fitted <- ans$m$fitted()
> cbind(x, y, fitted)
     x    y      fitted
[1,] 0 1.00 1.000000000
[2,] 2 0.81 0.800014044
[3,] 4 0.28 0.305655346
[4,] 6 0.10 0.055770323
[5,] 8 0.02 0.004859718
> plot(x, y, pch=19)
> x2 <- seq(0, 8, by=0.05)
> lines(x2, predict(ans, newdata=data.frame(x=x2)), col="red")
> points(x, predict(ans), col="red")

No.04697　Re: 非線形回帰曲線について　　【ぼのぼの】　2007/11/13(Tue) 14:55

御返事ありがとうございます。
なるほど，グラフを視覚的に把握しながら初期値を探すのですね。
やってみます。

それと今回の線形2次モデルではaとb共に正の中で動かせると理論的にフィットするのですが，aとbを正にするという条件をいれる場合，どのようにすればよいでしょうか。
それとも片方の値が0になってしまうだけでしょうか。
何度も申し訳ありませんがどうぞよろしくおねがいします。

No.04698　Re: 非線形回帰曲線について　　【青木繁伸】　2007/11/13(Tue) 15:48

パラメータに制約条件があるときは optim 関数
ただし，method="L-BFGS-B" で

> fun <- function(p)
+ {
+ 	return(sum((y - exp(-p[1]*x-p[2]*x^2))^2))
+ }
> x <- 0:4*2
> y <-  c(1, 0.81, 0.28, 0.1, 0.02)
> p <- c(1,0)
> ans <- optim(p, fun, method="L-BFGS-B", lower=c(0, 0))
> ans
$par
[1] 0.00000000 0.07033225

$value
[1] 0.005533373

$counts
function gradient 
      64       64 

$convergence
[1] 0

$message
[1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

今の場合は

> nls(y~exp(-b*x^2), start=list(b=1))
Nonlinear regression model
  model:  y ~ exp(-b * x^2) 
   data:  parent.frame() 
      b 
0.07032 
 residual sum-of-squares: 0.005533

Number of iterations to convergence: 8 
Achieved convergence tolerance: 8.626e-07

でもよさそうだが。いつもそうなるかは知らない。

No.04699　Re: 非線形回帰曲線について　　【ぼのぼの】　2007/11/13(Tue) 15:58

詳しい解説ありがとうございました！！
計算しなおしてみます。
Rについても，もっと精進したいと思います。