「統計学関連なんでもあり」の過去ログ--- 040

No.04441　回帰係数の差の検定？　　【難民】　2007/09/30(Sun) 17:44

統計検定の手法に関して質問させていただきます。

ある特定の被験者Aに対し，運動中の発汗量を計測しました。
条件は3要因で，
距離（40km/20km）走り方（マラソン/競歩）気温（5,10,20,40℃）
です。
各条件について，15回測定を行い，発汗量をy軸に，気温をx軸にとって
グラフを作成したところ，添付ファイルのようなグラフになりました。

（架空の実験設定なので，↑無理があるのですがお許しいただけると幸いですm(_ _)m）

私が確かめたいことは，
1）距離を固定したとき，走り方によって回帰係数に差はあるか？
（例えば，20kmのとき，マラソンの方が競歩より傾きが大きいか？）

2）走り方を固定したとき，距離によって回帰係数に差はあるか？
（たとえば，マラソンのとき，40kmの方が20kmより傾きは大きいか？）

3）距離によって，回帰係数に差はあるか？
（走り方に関わらず，40kmでは20kmに比べて傾きは大きいか？）

4）走り方によって，回帰係数に差はあるか？
（距離に関わらず，マラソンでは競歩に比べて傾きは大きいか？）

なのですが，いろいろ統計の本にあたったところ，
1）2）については，2条件を比較すればよいので，
回帰係数の傾きのt検定を行えばよいのではないか？と考えています。

ただ，3）4）のような場合，2要因の分散分析に似ており，
回帰係数の傾きのt検定を行うのは不適切に思えます。

（長くなりそうなので，コメントを改めて書き込みさせていただきます）

No.04443　Re: 回帰係数の差の検定？　　【難民】　2007/09/30(Sun) 18:02

【疑問1】
まず，私自身「問題があるのではないか？」と思うのは，
気温は"制御された"変数なので，回帰分析を行って，
フィッティングを行ったうえ，さらに傾きの差の検定を行って
よいのだろうか？という疑問です。

（私が回帰係数の差の検定なる手法を見つけたのは，
清水信博著「もう悩まない！論文が書ける統計」(OMS)（34ページから）で，
その本の中では，x軸は制御された値ではなく，ばらつくものになっています。）

【疑問2】
また，気温や距離は「数量的な変数」であり，単純に分散分析を
適用するのではなく，回帰係数の傾きに差があるのか，否かを調べたいと
考えております。

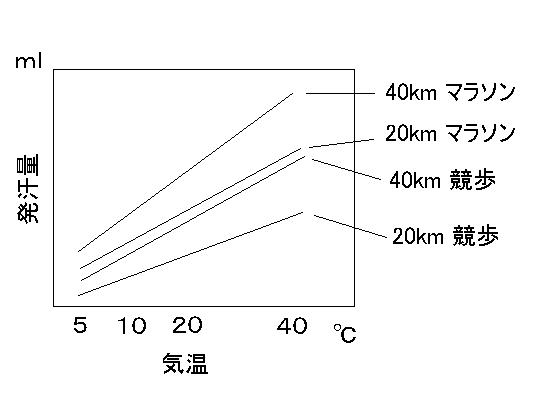
そしてさらに発汗量や回帰係数の傾きは，
走る距離（40km/20km）と数量的にどのような関係にあるのか？という点についても
分析をおこないたいと考えております。

上記の2つの疑問をまとめると，

（1）このような設定で回帰分析を行うのは適切か？

（2）不適切だとしたらどのような手法を用いれば，
気温や距離といった数量的な変数の効果を量的に分析できるのか？
（それとも，単純に分散分析をするしかないのだろうか？）

ということになります。

長々と書き込んでしまいましたが，アドバイスをいただけるとうれしく思います。

-------------------------------------------------
追伸

まずは，最初のコメント1）2）の内容を，回帰係数の差の検定を4回行うことで
たしかめたいと思います。（第一種の過誤の率が高まる？？）

3）4）については，それぞれの条件で平均値を出し（つまりデータを合成して），
回帰係数の差の検定を行ってみたいと思います。（データを合成するのはまずい？？）

この方法ではさすがに問題があるのだと思いますが…

No.04444　Re: 回帰係数の差の検定？　　【青木繁伸】　2007/09/30(Sun) 22:41

このように複雑な実験条件に対して，一変量解析的なやり方で物事を明らかにしようとするのが無理があるのではないでしょうか?

対象者が一人というのもどうかとは思いますが，
発汗量=a*距離+b*走り方+c*気温というモデル（必ずしも線形重回帰分析ではなく）という観点から説明していけばいかが?

No.04445　Re: 回帰係数の差の検定？　　【難民】　2007/10/01(Mon) 01:05

コメントありがとうございます。
このような場合に重回帰分析を行えばよいのですね！

あと，せっかく貴重なコメントをいただいたのに申し訳ないのですが，
あくまでも一変量解析的なやり方にこだわるとしたら，
どのような解決策が考えられますでしょうか？

実は共分散分析の平行性の検定が，私の目的に近いのではないかと
考えたのですが，

私の目的が「平行でないことを示したい！」であるのに対し，

共分散分析の場合は「平行でないと，そこで分析は終了！」となっており
（間違っていたらすみません），

平行でない場合，どことどこが平行でなかったかの多重比較などについて
論じられていないのです。
（少なくとも私の手元にある数冊の統計の教科書・参考書では）

さらなるアドバイスがいただければ幸甚です。

No.04446　Re: 回帰係数の差の検定？　　【難民】　2007/10/01(Mon) 01:30

さらにすみません。

この実験設定では，発汗量と気温は共変量ではなく，
気温については制御されたものなのですが，
回帰分析をして回帰直線をフィッティングすることは
妥当でしょうか？

（明日，重回帰分析に挑戦してみます！）

No.04448　Re: 回帰係数の差の検定？　　【太郎】　2007/10/01(Mon) 08:30

>平行でない場合，どことどこが平行でなかったかの多重比較などについて
論じられていないのです。

　ボンフェローニまたはその改良法（このサイトでよくでてくる統計的多重比較法の基礎参照）を用いて2処理ずつ回帰係数を比較するという方法があります。

　Tukey法を利用する方法もあるようですが，一般には紹介されていないようです。

No.04453　Re: 回帰係数の差の検定？　　【難民】　2007/10/01(Mon) 16:36

ありがとうございます。

＞このサイトでよくでてくる統計的多重比較法の基礎
とは，

統計的多重比較法の基礎，永田/吉田，1997，サイエンティスト社

ですね。ぜひ勉強したいと思います！
貴重な情報ありがとうございました。