「統計学関連なんでもあり」の過去ログ--- 040

No.04379　相関係数について　　【そら】　2007/09/20(Thu) 20:34

初めて質問させていただきます．最近統計の勉強を始めた初心者ですがよろしくお願いします．
相関係数rが1または－1に近いほど，「2つの変数の相関関係は強い」といえますが，このような場合，同様に「2つの変数の関連は強い」とはいえるのでしょうか．
また，「線形関係は強い」ともいえるのでしょうか．
相関係数と関連，線形関係についてうまく頭の中で整理できないでいます．
よろしくお願いいたします．

No.04380　Re: 相関係数について　　【青木繁伸】　2007/09/20(Thu) 21:34

> 相関係数rが1または－1に近いほど，「2つの変数の相関関係は強い」といえますが

一般的にはそうですが，相関係数の絶対値が1に近くても，2つの変数の相関関係がない場合もあります。
（a）の場合，ピアソンの積率相関係数は1に近いかも知れませんが，スピアマンの順位相関係数，ケンドールの順位相関係数は0に近いでしょう。
そして，二変数に相関関係はなさそうです。

> 「2つの変数の関連は強い」とはいえるのでしょうか

関連と相関関係の違いはなんでしょうか?関連の方が広義なのかな?あるいは逆に，因果関係のことを指しているのかな?因果関係だとすると，相関がいくら高くったって，因果関係があるわけではないことは明らかですね。
ピアソンの積率相関係数は，(b)のような場合には相関係数が1に近く，関連が強いといえるでしょうね。しかし，(c)のような場合にはスピアマンの積率相関係数は1よりは小さいが，二変数の関連は強いですよね（スピアマンの順位相関係数，ケンドールの順位相関係数は1に近い）。

> 「線形関係は強い」ともいえるのでしょうか

ピアソンの積率相関係数は線形の関係の強さを測るのだから，絶対値が1に近いほど線形関係が強いことを表します。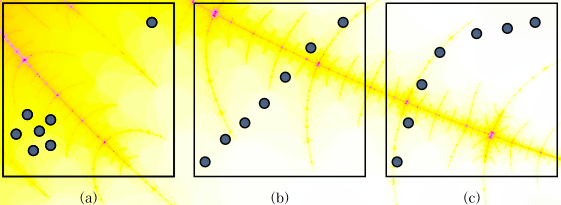

No.04381　Re: 相関係数について　　【そら】　2007/09/21(Fri) 20:15

青木先生，わかりやすい解説ありがとうございます．
線形関係についてはピアソンの積率相関係数のときのみいえることなのですね．
スピアマンの順位相関係数の場合は線形関係ではなく，なにかしらの関数のような形になっていれば2変数の関連が強いといえるということでよろしいでしょうか．

No.04382　Re: 相関係数について　　【青木繁伸】　2007/09/21(Fri) 21:04

> スピアマンの順位相関係数の場合は線形関係ではなく，なにかしらの関数のような形になっていれば2変数の関連が強いといえるということでよろしいでしょうか

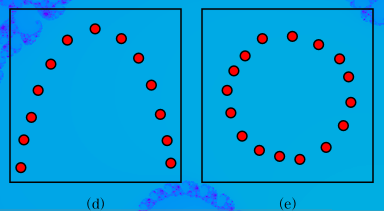
だめです。単調増加か単調減少の場合だけ相関は1になります。
前の図の(c)のような場合。
(d)，(e)のような場合は関連は非常に強いが相関はほぼ0でしょう（ピアソンの積率相関係数も，スピアマンの順位相関係数の場合にも。