「統計学関連なんでもあり」の過去ログ--- 040

No.04297　正規分布が生じる原因について　　【Mike】　2007/08/31(Fri) 22:44

2変量x,yに関するデータがある状況で，yをランダムに並べ替えて，x,yの内積（データ列をベクトルとみなして）を計算する試行を繰り返しました。

データ数をN,試行回数をMとすると，N,Mともに十分大きい場合（目安は
N>=20,M>=10000），x,yの分布に関わらず，得られる内積はほぼ正規分布に従うという結果になりました。

これがなぜなのか，考えているのですが，式で示すための糸口がつかめません。
何かご指摘をいただければ嬉しく思います。
よろしくお願いいたします。

No.04298　Re: 正規分布が生じる原因について　　【青木繁伸】　2007/08/31(Fri) 23:08

たいていの操作をしても，結果は正規分布に近くなるのではないでしょうか?
要するに，「誤差」の集積で，誤差関数，正規分布になるのでは?

sum(log(x)*sample(x)) も sum(sqrt(x)*sample(x)) も sum(exp(x)*sample(x)) だって，正規分布みたいな分布になりますよねぇ
N <- 30
M <- 10000
x <- runif(N)
y <- runif(N)
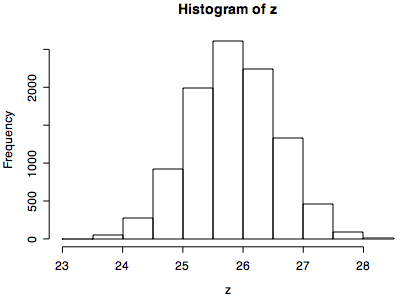
z <- sapply(1:M, function(i) sum(exp(x)*sample(y)))
hist(z)

No.04299　Re: 正規分布が生じる原因について　　【Mike】　2007/09/01(Sat) 01:47

早速ご回答をいただきありがとうございます。
正規分布のような分布は，本当に色々なところに登場するのですね。
式で証明すべき問題だと思い込んでいたのですが，中心極限定理というもので理解すべきなのでしょうか。もう少し勉強してみます。

No.04301　Re: 正規分布が生じる原因について　　【Mike】　2007/09/03(Mon) 00:56

数値実験を進めた結果，上述の内積が従う正規分布は，平均がN*mean(x)*mean(y),分散がN*var(x)*var(y)の分布であることがわかりました．ここで，mean(), var()は，ベクトルの要素の平均および標本分散を表します．

上述の内積をNで割ったものをaとし，ベクトルx,yのある要素どうしの積を新しい変数zとおくと，zはN!>>N通りあるので，aはzの標本平均（標本数N）とみなすことができるかもしれないと考えました．この前提に従えば，中心極限定理より，Nが十分大きいとき，aはほぼ平均がmean (x)*mean(y), 分散が(var(x)*var(y)+var(x)*mean(y)^2+var(y)*mean(x)^2)/Nの正規分布に従うことが導かれました．平均に関しては第1段落に記した結果と一致しますが，分散が一致しませんでした．

以上，下記URLにまとめました．
http://sky.geocities.jp/hyman1919/xy_norm.htm

No.04310　Re: 正規分布が生じる原因について　　【のね】　2007/09/03(Mon) 23:06

横から失礼します。

> 分散がN*var(x)*var(y)

には疑問があります。今，x を固定して考えると，

x=100 -> var(xy)= 100^2*var(y)
x=1000 -> var(xy)=1000^2*var(y)

となり，Mikeさんの後の法の計算と一致するはずです。

No.04314　Re: 正規分布が生じる原因について　　【Mike】　2007/09/05(Wed) 10:20

貴重なご指摘をいただきありがとうございます。
「xを固定する」とは，ベクトルxの要素を全て一定値とする意味に解釈してよろしいでしょうか。

すみません，ベクトルを小文字で表現してしまったのがまずかったと思います。実は，x,yはベクトルのつもりでした。var(xy)はxとyの内積の分散を意味します。したがって，例えばxの要素が全て100で等しい場合，内積x・yの分散は，「yの総和の100倍」の分散となり，0になることが理解されます。

実際に数値実験を行ったところ，分散は0となり，N*var(x)*var(y)に一致しました。

No.04321　Re: 正規分布が生じる原因について　　【のね】　2007/09/05(Wed) 23:54

私が間違いですね。後の式の導出に気をとられて，並べ替えの部分を読み間違えました。
とすると，計算式の導出が間違っているとしか思えませんが，回答が思い浮かびません。

すみませんでした。

No.04322　Re: 正規分布が生じる原因について　　【のね】　2007/09/06(Thu) 23:11

最後の部分に飛躍があるような気がしますが，

x0=mean(x)，y0=mean(y)として，x=x0+dx，y=y0+dy とおく．ここで，x0，y0は定数，dx，dyはベクトル，Sum(dx)=Sum(dy)=0 である．したがって，

z = sum(xy)=sum((x0+dx)(y0+dy))
= Nx0y0+x0*Sum(dy)+y0*sum(dx)+sum(dxdy)
= Nx0y0+Sum(dxdy)

∴　E(z) = Nx0y0+E(sum(dxdy)) = Nx0y0
　　V(z) = V(z-Nx0y0) = V(Sum(dxdy))
　　　　 = Sum(V(dx)*V(dy))
　　　　 = N*V(dx)*V(dy)

というのはいかがでしょうか。