No.03768　χ2乗検定とFisherの直接法について　　【田村】　2007/06/26(Tue) 11:00

はじめまして。
初歩的な質問で申し訳ありません。

χ2乗検定とFisherの直接法の違いについて教えてください。どういうときにどちらを使えばよろしいでしょうか？また，正確確率検定は，期待度数が5未満のセルが20%以上存在する場合に用いるという認識でよろしいでしょうか？
No.03769　Re: χ2乗検定とFisherの直接法について　　【青木繁伸】　2007/06/26(Tue) 11:16

どんな場合にも，Fisher の直接法を使えばよいです
（計算に時間が掛かりすぎたり，メモリー不足でコンピュータで求められない場合にのみカイ二乗漸近近似法を使う）
No.03776　Re: χ2乗検定とFisherの直接法について　　【kai】　2007/06/26(Tue) 16:29

Fisherの正確確率検定は名前の通り正確に確率を計算しています．
近似的な方法は全く使われていないので，青木先生がおっしゃっているように，使えるなら正確検定がいです．EXCELでは数値が大きくなると桁数オーバーでエラーが出やすいです．．．
No.03777　Re: χ2乗検定とFisherの直接法について　　【青木繁伸】　2007/06/26(Tue) 17:11

Excel でやれる範囲のものは2×2分割表でのものでしょう。その場合の注意点としては，
http://aoki2.si.gunma-u.ac.jp/lecture/Cross/fisher-calc.html
があります。
2×2分割表よりも大きな場合については，Rを使うのが一番簡単です。
No.03779　Re: χ2乗検定とFisherの直接法について　　【田村】　2007/06/26(Tue) 20:32

ありがとうございます。
SPSSでχ2乗検定を行うとき，正確確率検定を選ぶと，「Fisherの直接法」による正確有意確率とPearsonのχ2乗による正確有意確率が表示されます。
Fisherの直接法による正確有意確率とはどちらのことでしょうか？
No.03780　Re: χ2乗検定とFisherの直接法について　　【青木繁伸】　2007/06/26(Tue) 21:25

さて，「Pearsonのχ2乗による正確有意確率」って表記になっていますか？
できれば，実際の例とその分析結果を呈示してください

たとえば，以下の分割表ではどうなりますか？
5　　9
4　　3
No.03783　Re: χ2乗検定とFisherの直接法について　　【田村】　2007/06/27(Wed) 12:09

SPSSにてΧ二乗検定をえらび，正確確率をチェックすると以下のようになりました。
カイ2乗検定

　　　　　　　漸近有意確率(両側)　正確有意確率(両側)　正確有意確率(片側)

Pearson
のカイ2乗	　　　　0.34，　　　　　　　　0.6424，　　　　　0.31885	

連続修正
　(a)	　　　   　0.63
			
尤度比	　　　　0.35，　　　　　　 　　0.6424，　　　	0.31885	

Fisherの
直接法　　　　　　　　　　　　　　　   　 0.3972，　     　0.31885	

有効なケースの数	21					

a	2x2 表に対してのみ計算
b	2 セル (50.0%) は期待度数が 5 未満です。最小期待度数は 3.00 です。
c	標準化統計量は -.913 です。
No.03784　Re: χ2乗検定とFisherの直接法について　　【UJ】　2007/06/27(Wed) 12:33

割り込み済みません．
上記の"a 2x2 表に対してのみ計算"についてですが，
2×3等の頻度集計の際に，期待度数が5未満のセルが複数存在する場合は，
χ2乗検定で比較を実施すればよいのでしょうか．
No.03785　Re: χ2乗検定とFisherの直接法について　　【青木繁伸】　2007/06/27(Wed) 13:22

> 2×3等の頻度集計の際に，期待度数が5未満のセルが複数存在する場合は，
> χ2乗検定で比較を実施すればよいのでしょうか．

No.3769で，
> どんな場合にも，Fisher の直接法を使えばよいです

と書いたように，いつも Fisher の正確確率検定を行えばよいだけです
R を使えばよい
No.03789　Re: χ2乗検定とFisherの直接法について　　【青木繁伸】　2007/06/27(Wed) 14:17

Fisher の直接法の正確有意確率とは，観察された分割表の生起確率よりも小さい生起確率を持つ分割表の生起確率を合計したものを P 値とします。

Pearson のカイ二乗法の正確有意確率とは，観察された分割表のカイ二乗値以上の値を持つ分割表の生起確率を合計したものを P 値とします。

Fisher は前者のように定義した。2×2分割表の場合には生起確率とカイ二乗値が逆比例しているので問題は大きくない（ほとんどの場合両者は同じ結果を与えるが，食い違いが生じることも少なからずあり，その食い違い方は甚だしいものになることが多い）。
しかし，2×2より大きい分割表を対象にする場合，生起確率が小さいものを足すということは不合理と考えられる。

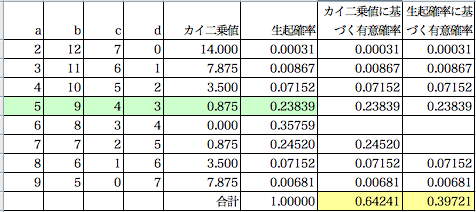
No.3780，3783 の計算例（クリックすると原寸表示）

fig

● 「統計学関連なんでもあり」の過去ログ--- 040 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る