No.03418 Re: 曲線の当てはめと次数の打ち切り 【takahashi】 2007/05/22(Tue) 18:53
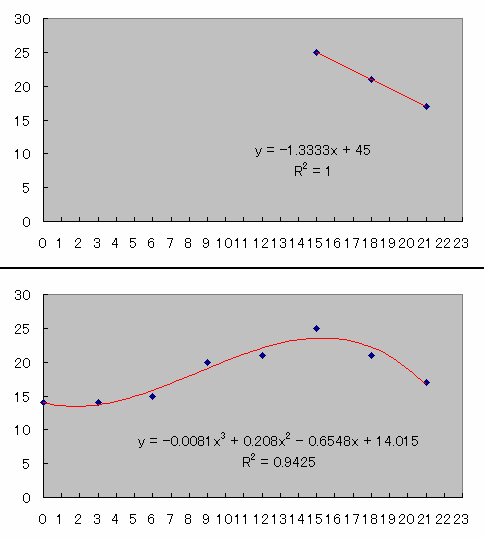
>それから,曲線を当てはめていく場合,次数を上げていけば上げていくほど(見かけ上は)当てはまりが良くなりますが,次数の打ち切りの目安というのはあるのでしょうか。
「モデル選択」をキーワードに検索してみるのがよいかと。
No.03423 Re: 曲線の当てはめと次数の打ち切り 【青木繁伸】 2007/05/22(Tue) 22:23
> すべてのデータに対して当てはめを行うのが適切か?。。。推定したい付近の時刻を選んだデータに対して当てはめを行うのが適切か?
後者でしょう。推定したい部分とそうでない部分が別の関数に従うなら全部を使えば,そのどれとも違う関数に当てはまってしまうでしょう。
場合によっては,データをいくつかの区分に分けて,それぞれの区分ごとに当てはめる場合もありますからね(ホッケースティックモデル。。。二本の回帰直線で当てはめ)
多項式回帰の次数の選択については,AIC とかなんとかを参照。
No.03425 Re: 曲線の当てはめと次数の打ち切り 【波音】 2007/05/22(Tue) 23:28
takahashi先生に青木先生,早速の回答ありがとうございました。
モデル選択というキー ワードで検索してみたら,AICとかBIC,MDLなどが出て来ました。以前から,色々な場面でこれらの単語を目にはしていましたが,実際に使う機会がな かったので素通りしていました。・・・が,これをきっかけに早速,図書館へ行って何冊か本を読んでみたいと思います。
> 場合によっては,データをいくつかの区分に分けて,それぞれの区分ごとに当てはめる場合もありますからね
自分の中ではある直線(あるいは曲線)が上手く当てはまりそうな所を抜き出して当てはめるようなことは,"卑怯な振舞い"かとも考えていたのですが,間違えさえしなければ正当な方法だったのですね。
ここのところ,統計の勉強がサボりがちだったのですが,新たな課題が出てきてうれしく思います。
No.03426 Re: 曲線の当てはめと次数の打ち切り 【青木繁伸】 2007/05/22(Tue) 23:36
理論的な裏付けがあることが前提であることはいうまでもありません
気温の例でも午前中の上昇傾向期,午後の下降傾向期みたいなモデルが妥当と言うことであれば,複数の直線で当てはめたり,三角関数みたいに周期的に動くというモデルなら三角関数に当てはめればよいし。
No.03454 Re: 曲線の当てはめと次数の打ち切り 【kkk】 2007/05/24(Thu) 20:14
気温が安定している頃(例えば前日の0時も翌日の0時もほぼ同じ)の記録値であれば,フーリエ解析にもってこいの例と思います。
一応フーリエ変換により補間を試みた結果を図にしてみました。(ただし0時は14℃に変更しています。)
誤差の原因として以下の要因が考えられます。9時に20℃というのが少し珍しいように思えますし,1℃単位に丸めているのが少し大雑把すぎではとも思います。また3時間間隔が粗すぎということも考えられます。
No.03459 Re: 曲線の当てはめと次数の打ち切り 【波音】 2007/05/26(Sat) 11:16
kkk先生,回答ありがとうございます。
「フーリエ変換」。。。 大学1年生のときに興味本位で少しだけ勉強した記憶がありますが,今となっては図をみても正直わからない状態です。なので,ちょっとフーリエ解析について調べてみようと思います。
+-----+-----+-----+
そ れでここからは別の質問になるのですが,とりあえず自分で適当なデータを作って2次曲線と3次曲線を当てはめる作業をし,それぞれRのAIC()でAIC を出してみました。AICの値は小さいほど良いようですが,-Infという結果が返ってくる場合はどう解釈すればよいのでしょうか?
普通に考えれば「限りなく小さい」という意味で良いモデルであるとも考えたのですが,どういうことでしょうか。
x <- c(12, 15, 18, 21)
y <- c(56, 46, 59, 70)
x2 <- x^2
result <- lm(y ~ x2 + x) #2次式の場合
x3 <- x^3
result2 <- lm(y ~ x3 + x2 + x) #3次式の場合
#データのプロット(曲線の重ね描き)
plot(x,y,col="blue",pch=19)
xx <- seq(12,21,0.01)
points(xx, 179.7500 + 0.5833*xx^2 - 17.4167*xx, pch=".") #2次曲線のプロット
points(xx, 826.0000 - 0.1543*xx^3 + 8.2222*xx^2 - 140.6111*xx, pch=".",col="pink") #3次曲線のプロット
No.03460 Re: 曲線の当てはめと次数の打ち切り 【takahashi】 2007/05/26(Sat) 12:31
プロットを見ればわかるかと思いますが,残差が0ということです。
No.03461 Re: 曲線の当てはめと次数の打ち切り 【波音】 2007/05/26(Sat) 15:28
なるほど,曲線が完全にのっかっているということですね。ありがとうございました。
No.03483 Re: 曲線の当てはめと次数の打ち切り 【kkk】 2007/05/28(Mon) 20:03
エクセルにも「ツール」→「分析ツール」の中に「フーリエ解析」というのが追加でインストールできると思います。
その結果と下図の係数を比較すると,0次と第4次高調波の係数がフーリエ解析結果の1/8,
第1〜第3次高調波の係数が1/4になっていることが分かるかと思います。
私の最初の図では,第4次高調波の係数を1/4にしていたため元のデータからのズレが生じたようです。
(今まで計算ミスをしていたようです。)ただ,気温の変化として見ると第4次高調波を0にした方が自然な感じがするので,やはり丸め誤差の影響が第4次高調波に現れているのではないかと思われます。
ちなみに観測点の近くに大きな発熱源が無く,またその日に急激な気温変化を起こす現象が生じていなければ,
通常は,次数が高い成分の係数はほとんど0になります。
また丸め誤差は次数が高い成分の係数ほど大きくなる性質がありますので,第4次高調波を0にする(0に近づける)ことはそれほど不適切な処理ではないのではないかと思われます。
No.03486 Re: 曲線の当てはめと次数の打ち切り 【青木繁伸】 2007/05/28(Mon) 22:46
0 のときは,4 じゃなくて,14 なんですね?
全ての点を通る曲線という意味なら,フーリエ解析とか高次多項式も有用かも知れませんが,スプライン曲線という手もある。
もっとも,それらのうちで,より適切なものはあるだろう。time <- c(0, 3, 6, 9, 12, 15, 18, 21)
temp <- c(14, 14, 15, 20, 21, 25, 21, 17)
ans <- spline(temp~time)
plot(ans, type="l")
lines(temp~time, col="red")
No.03487 Re: 曲線の当てはめと次数の打ち切り 【青木繁伸】 2007/05/28(Mon) 22:52
データを繰り返して,もう少し細かく当てはめるtime <- 0:15*3
temp <- c(14, 14, 15, 20, 21, 25, 21, 17, 14, 14, 15, 20, 21, 25, 21, 17)
ans <- spline(temp~time, n=10*length(time))
plot(ans, type="l")
lines(temp~time, col="red")
No.03501 Re: 曲線の当てはめと次数の打ち切り 【kkk】 2007/05/29(Tue) 15:56
>また丸め誤差は次数が高い成分の係数ほど大きくなる性質がありますので,
これは私の思い込みでした。
今回いろいろ丸め誤差を作って試したところ,ほとんどホワイトノイズと思える挙動が観測されました。
したがって第4次高調波を0にすることの強い根拠は無くなりました。
ホワイトノイズ:いずれの周波数成分の強度もほとんど同じである性質のノイズ。
光として観測すればほとんど色がつかないことからこう呼ばれる。
● 「統計学関連なんでもあり」の過去ログ--- 040 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る