「統計学関連なんでもあり」の過去ログ--- 040

No.03206　チップ内部の素子の最大値の分布に関して　　【きくち】　2007/04/13(Fri) 19:10

はじめまして，半導体メモリーのエンジニアをやっているものです。
このたびは，半導体メモリーの最悪素子のばらつきに関して，質問させてください。

半導体メモリーのチップの中には，1メガ個～10ギガ個の記憶素子があります。
この素子は閾値電圧という量で管理していまして，これらはチップ内部で正規分布をしています。

半導体メモリーにとって，最も閾値電圧が高いものや低いものが，製品としての最悪素子になります。
言い換えますと，これらの素子が，チップ自体の特性を決めてしまいます。
つまり，大量のチップを作り，これらの特性を予想する場合には，
このチップの最大値・最小値がどういう分布になるかが知りたいところです。

実際，このチップの閾値電圧の最大値が，どういう分布になるのかを計算をしてみました。
質問は，この考え方が，正しいか教えていただきたいです。

いろいろ調べて見たのですが，同じような問題を見付ける事ができませんでした m(_ _)m。
その為，相談させていただきました。よろしくお願いいたします。

計算内容

<<< 前提条件 >>>
- Chip内部の素子数が，n個とします。
- Chip内部の素子は，平均値μ，標準偏差σで分布しているとします。
　ここで，正規分布をf(V)，累積正規分布をF(V)とおきます。

<<< 計算方法 >>>
(0) 最大値が，Vmaxである場合を考えます。
(1) 正規分布を，
　　「最大値を含む区間」　（ここは無限小の区間幅とします。）
　　「最大値より大きい閾値電圧を含む区間」
　　「最大値より小さい閾値電圧を含む区間」
　の3つに分けて考えます。
(5) 最大値Vmaxが発生する確率　g (Vmax)　を考えると，
　「最大値を含む区間」では1回発生　（無限小区間なので2回以上発生する場合は無視できる。）
　「最大値より小さい閾値電圧を含む区間」ではn-1回発生
　「最大値より大きい閾値電圧を含む区間」では，0回発生
　　したということなので，多項分布から，
　　g (Vmax) = nC1 x ( f (Vmax) ) x ( F (Vmax) )^(n-1)
　　　※nC1は，コンビネーションです。
　　となります。

<<< 結果 >>>
最大値の分布は，n，μ，σに依存。

この考え方は，正しいのでしょうか？
申し訳ありませんが，教えてください m(_ _)m。

No.03207　Re: チップ内部の素子の最大値の分布に関して　　【青木繁伸】　2007/04/13(Fri) 19:36

シミュレーションでやってみました
> x <- sapply(1:1000, function(i) max(rnorm(1000000)))
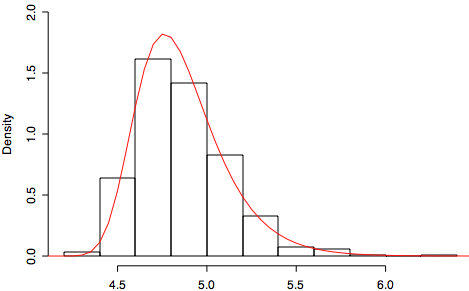
> hist(x,prob=TRUE, ylim=c(0,2))
> z <- seq(4, 7, by=0.05)
> y <- 1000000*dnorm(z)*pnorm(z)^(1000000-1)
> lines(z, y, col="red")
良さそうな感じですかね。

No.03218　Re: チップ内部の素子の最大値の分布に関して　　【ファン】　2007/04/14(Sat) 18:51

No.3206
>この考え方は，正しいのでしょうか？

「順序統計量」の分布，例えば Wikipedia
http://ja.wikipedia.org/wiki/%E9%A0%86%E5%BA%8F%E7%B5%B1%E8%A8%88%E9%87%8F
において，「最大値」のケースを考えると，結果は正しいですね。

しかし最大値だけなら，以下のように考えた方が簡単かと，，，

　閾値電圧の最大値が Vmax "以下"である確率 G(Vmax) は
　　　G(Vmax) = F(Vmax)^n　（ただし n 個が独立または無相関な場合）
　よって，その確率密度関数 g(Vmax) は
　　　g(Vmax) = dG(Vmax) / dVmax = n・[F(Vmax)^(n-1)]・f(Vmax)

また，分布が現実と合うかどうかは，同一チップ内の n 個の素子の特性が，独立または無相関（正規分布なら同等）に近いかどうかによるでしょうね。

No.03224　Re: チップ内部の素子の最大値の分布に関して　　【きくち】　2007/04/16(Mon) 09:27

青木さん，ファンさん，ご検討をありがとうございます。
間違ってなかったようで良かったです(^_^;A。
ありがとうございました。