No.03168 Re: 正規分布? 【青木繁伸】 2007/04/10(Tue) 18:52
たとえばの例として,誤差を産む原因が温度だとしませんか。
温度が高くても低くても誤差を産む。ちょうど良い温度の時が誤差が一番小さい。
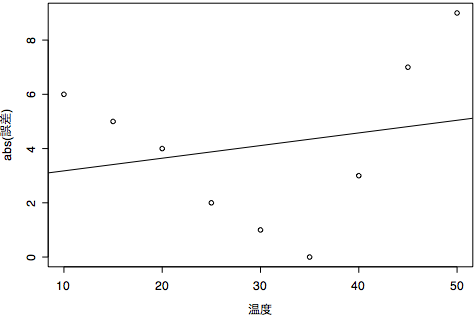
以下のようなデータがあるとしましょう。
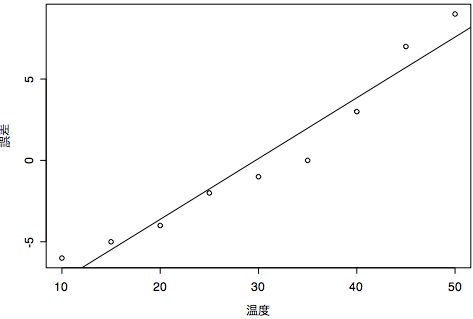
温度 誤差誤差の絶対値を取ってプロットし,回帰直線を求めると以下のようになりますよ。
1 10 -6
2 15 -5
3 20 -4
4 25 -2
5 30 -1
6 35 0
7 40 3
8 45 7
9 50 9
これが求める解でないだろうことは明らかですね。
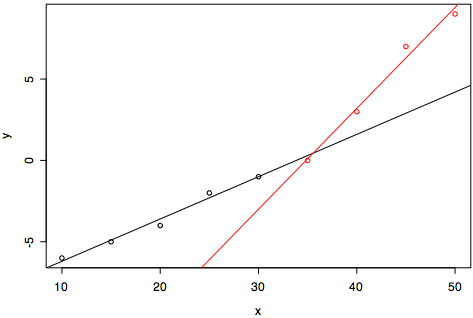
誤差がマイナスになるときとプラスになるときに分けて,二本の回帰直線を求めると,その交点の温度の時にたぶん誤差が一番小さくなるとか?