No.02500 十分推定量 【まこりん】 2007/01/28(Sun) 18:57
十分推定量がよくわかりません。
推定量をTとして,母数をαとすると
Πf(xi)=g(T|α)×h(x1,…xn){gは密度関数}だと思うのですがこれがいったい何を意味しているのかかわりません。
No.02528 Re: 十分推定量 【ファン】 2007/01/30(Tue) 00:41
その表現の場合,統計量 T を与えた時の条件付き確率 h(x1,…,xn) が推定する母数 α に依存しないこと,というのが「十分統計量」の定義です。式全体は,条件付き確率の定義から導かれる一般の乗法定理
Pr{ A かつ B } = Pr{ A }×Pr{ B | A }
を,標本 {x1,…,xn} とその統計量 T について適用した形になっていますよね。
な
ぜそんな性質を考えるのかというと,データをある側面から要約した時,その要約中に母数 α
の推定に役立つ情報の"すべて"が含まれているかどうかを確認するためです。例えば,ニュースの見出しに惹かれて記事を読んでみたところ,知りたかったポ
イントについて見出し以上の情報が含まれていなかった場合,その記事は見出しが十分統計量で(見出しを知った後に読んだ)本文はゴミ(汗。
[より数学的な定義や例] http://mp-w3math.jwu.ac.jp/~konno/pdf/statr28.pdf
No.02596 Re: 十分推定量 【まこりん】 2007/02/02(Fri) 22:04
本をよんだところh(x1,…,xn) は確率ではないような気がします。私の推論なのですが
Πf(xi)/g(T|α)=h(x1,…xn)(hは密度関数ではない)
と
かけるということはαについてΠf(xi)を微分することと,g(T|α)を微分することは等しい。つまりΠf(xi)の最尤推定量とg(T|α)のαで
の微分した答えは等しく,また同時にg(T|α)のαでの微分した答えが,α=Tとなるならばそれを十分推定量というのでは?
つまり十分推定量は最尤推定量の一部なのでは?と思うのですがどうなのでしょうか?
No.02598 Re: 十分推定量 【ファン】 2007/02/04(Sun) 18:09
>本をよんだところ h(x1,…,xn) は確率ではないような気がします。
A「十分統計量 T の定義(意味的)」(記号一部補足変更)
統計量 T を与えた時の標本 {x1,…,xn} の条件付き確率
= [同時確率 f(x1,…,xn;α)] / [Tの確率 g(T;α)] = h(x1,…,xn;α)
において『h が α に依存しないこと』。すなわち
= h(x1,…,xn)
ただし f が確率密度なら g, h も確率密度。
なら,h は確率(密度)そのものですよね。一方
B「その必要十分条件(Fisherの分解定理:発見的 & 形式的)」
同時確率 f(x1,…,xn;α) = g(T;α) h(x1,…,xn) なる分解 g, h が存在する
だと,分解を決める時に,定数部と「T に依存し α に依存しない部分」とを,g が T の確率(密度)になるように調整すれば,h は条件付き確率(密度)。
[ベルヌーイ分布例] http://www.is.seikei.ac.jp/~iwasaki/kouginote/B/B.03.One-Sample/B.03.1.Statistic.htm
>つまりΠf(xi)の最尤推定量とg(T|α)のαでの微分した答えは等しく,
鋭いですね。言葉で表すと…(スカラーの)十分統計量が存在すれば,最尤推定量は十分統計量の関数になる。また逆関数を持てば,最尤推定量自身が「十分性」(十分統計量であること)を持つ。
つ
まり,客「いい推定量あります?」店員「最尤推定量でわ?」客「なにそれ?」店員「"一致性","有効性"といった実際面からの優秀な性能に加えて,狙っ
た母数成分を標本から 100% 抽出する"十分性"と呼ばれる保障機能が内蔵されておりまして,使い方も簡単,価格もお手頃…」客「それ下さい!」
No.02924 Re: 十分推定量 【まこりん】 2007/03/04(Sun) 17:23
gが密度関数ならばhも密度関数といえるならば,
∬…∬h(x1,x2,…xn)dx1dx2…dxnは1になるはずですよね。
仮にx1からxnが正規分布N(μ,σ^2)に従うとし,T=(x1+x2‥+xn)/nとすると,g(t|μ)=(n/2nσ^2)^(1/2)exp{-n(t-μ)^2/2σ^2}⇒tで積分すると1になるので確率密度関数
では
h(x1,x1,x2,…xn)=1/n^(1/2){1/(2π)^(1/2)σ}^(n-1)exp{-Σ(n,i=1){xi-(x1+x2‥+xn)/n}^(2)/2σ^2}
はx1…xnで積分すると1になるのでしょうか?ならなければ確率密度関数とはいえませんよね?n=3ぐらいでご教授願いたいのですが。
No.02935 Re: 十分推定量 【ファン】 2007/03/05(Mon) 19:08
>∬…∬h(x1,x2,…xn)dx1dx2…dxnは1になるはずですよね。
えっとそ
の部分が違います。その扱いだと,分解によって次元が増加してしまいますから(x1,…,xn ⇒ T, x1,…,xn )。十分統計量
T(x1,…,xn) を独立した変数として扱う時には,h(x1,…,xn) の定義域が制約されます。例えば T = x1 + … + xn
なら,n 次元空間の中の(T の値が等しい) n - 1 次元超平面の点のみで,関数値 h(x1,…,xn)
を考える必要があるわけです。また統計的には,そのことが T を与えた時の「条件付き分布」を意味します。
>n=3ぐらいでご教授願いたいのですが。
以下に一番簡単な n = 2 の場合を書きました。n = 3 以上は有償で…(笑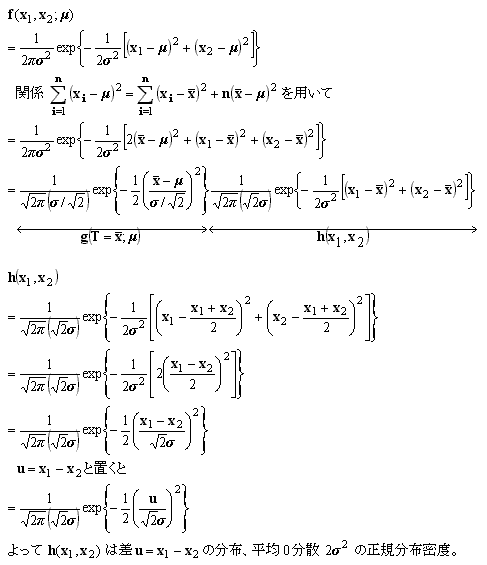
No.02972 Re: 十分推定量 【まこりん】 2007/03/10(Sat) 23:08
>例えば T = x1 + … + xn なら,n 次元空間の中の(T の値が等しい) n - 1 次元超平面の点のみで,関数値 h(x1,…,xn) を考える必要があるわけです。また統計的には,そのことが T を与えた時の「条件付き分布」を意味します。
これはTがきまるとx1からxnのうちのn-1個しか自由に動けないってことですよね。
これがh(x1,x2)の確率変数が(x1-x2)になるということにどうつながってくるのでしょうか?ちなみにn=3以上では確率変数は何になるのでしょうか?
No.02978 Re: 十分推定量 【ファン】 2007/03/11(Sun) 23:44
>これはTがきまるとx1からxnのうちのn-1個しか自由に動けないってことですよね。
そ
うですね。標本平均のケースで T = (1/2)(x1 + x2) なら,(x1, x2) = (x1, 2T-x1) = (0, 2T) +
(1, -1)・x1 において x1 のみを変化させた軌跡,つまり x1 を横軸 x2 を縦軸とする平面上の切片 2T 傾き -1
の直線がその集合です。
したがって,h(x1, x2) はその直線上に定義されている確率密度であり,一変量の確率分布ですが,斜めの直線上に乗っているため x1 を変数とすると扱いが少し面倒になります。(一般にはヤコビ行列式の知識が必要)
>これがh(x1,x2)の確率変数が(x1-x2)になるということにどうつながってくるのでしょうか?
同じく x1 を横軸 x2 を縦軸とする平面上に,T = (1/2)(x1 + x2) 軸と u = x1 - x2 (または x2 - x1) 軸を描き,先の直線上の点を考えると…
>ちなみにn=3以上では確率変数は何になるのでしょうか?
それは有償情報なのでヒントのみ(笑。n = 3 の場合には
a・x1 + b・x2 + c・x3 (ただし a + b + c = 0)
のような一次式で表される確率変数2つになります。(n = 4 以上も同様)
● 「統計学関連なんでもあり」の過去ログ--- 040 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る