No.01247　視聴料の合計　　【水島】　2006/10/06(Fri) 22:41

先ほど投稿したのですが，宿題の答えを求める記事と判断されたようで，私の研究の内容が具体的に公にできない事情がありまして，問題風に変えて表現したのがいけませんでした。ごめんなさい。再度質問をお許しいただきましたら幸いです。

n人の母集団にアンケートをして。p(i)の確率で，a(i)ドルの視聴料を集められる（1-p(i)の確率でゼロ）というデータが集まりました（i=1,n）。ここで，

n人の視聴料の合計が，80%信頼区間（10%〜90%）の合計視聴料の区間を求めたい。
また，n人の視聴料の合計がAドル以下である確率Pを求めたい。
ちなみに　n>100です。二項分布を拡張すればできるのではと考えてやってきましたが，挫折し，プログラムで総当りで確率分布を生成することには成功しました。しかし，このやり方だと，せいぜいn<16程度なので困っております。

どうぞよろしくお願いいたします。
No.01248　Re: 視聴料の合計　　【青木繁伸】　2006/10/06(Fri) 23:27

> n人の母集団にアンケートをして。p(i)の確率で，a(i)ドルの視聴料を集められる（1-p(i)の確率でゼロ）というデータが集まりました（i=1,n）。

という記述が不正確で良く理解できないのですが，
「n人の母集団」というのは，「n人に対するアンケートで」，「自分ならxドル払える」というデータを集計して，たとえば「0ドル払う人はa0%，1ドル払う人はa1%，2ドル払う人はa2%,,,」というデータがあるということですか？
そして，たくさんの人に対してこの確率を適用して得られる視聴料の信頼区間などを求めたいと？

シミュレーションというのも一つの解かと。
> simulation <- function(limit, n=500, loop=1000)
+ {
+ 	# $0:0.1, $1:0.2, $2:0.3, ...
+ 	a <- c(0.1, 0.2, 0.3, 0.2, 0.1, 0.05, 0.03, 0.02)
+ 	result <- sapply(1:loop, function (i) {
+ 	  x <- cut(runif(n), breaks=c(-Inf, cumsum(a), Inf),
+                  right=FALSE)
+ 	  sum(table(x)*0:8)
+         })
+ 	result <- sort(result)
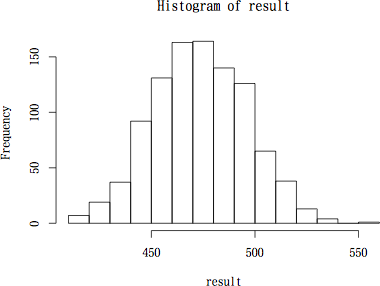
+ 	hist(result)
+ 	return(list(lo=result[0.2*loop], hi=result[0.8*loop],
+              p=sum(result<limit)/loop))
+ }
> simulation(440, n=200, loop=1000)
$lo
[1] 454

$hi
[1] 495

$p
[1] 0.053

fig

No.01249　Re: 視聴料の合計　　【水島】　2006/10/07(Sat) 00:51

早速の回答ありがとうございました。また，表現が不正確ですみませんでした。もう少し詳しく書こうと思います。

ある番組を視聴する契約をした100人に番組のサンプルを見せた後アンケートしました。
質問1：いくら払いますか？
質問2：実際の番組を見て，その金額を払う確信はどの程度ですか
0％（確実に払わない）
10％，20％・・・80％，90％
100％（確実に払う）
から選んでください。

ということで，金額と確率（確信）のペアが100サンプルあるということです。
ここでは，回答者の確信（確率）は正しいものと仮定しています。例えば，80%と回答した人が10人いた場合，結果として8人は払い，2人は払わないということです。また，回答は一人につき一組（金額と確率）としています。

例えばN=3のとき，
1番目の人は，p(1)=25%, a(1)=$50
2番目の人は，p(2)=60%,a(2)=$25
3番目の人は，p(3)=80%,a(3)=$30
と回答したとすると。

25%*60%*80% の確率で，$105(50+25+30)・・・全員払う
25%*60%*20% の確率で，$75(50+25)・・・3番目の人は払わない
　　：
75%*40%*20% の確率で，ゼロ・・・全員払わない。

という確率分布になります。組み合わせは2の3乗になります。nが大きいとき，この確率分布における80%信頼区間などが欲しいんです。

よろしくおねがいします。
No.01252　Re: 視聴料の合計　　【青木繁伸】　2006/10/07(Sat) 09:03

問題設定が過剰に精度を設定していると思いますね。
支払いの確信が余計で，じゃまをしていると思います。

> 25%*60%*80% の確率で，$105(50+25+30)・・・全員払う
> 25%*60%*20% の確率で，$75(50+25)・・・3番目の人は払わない

払う・払わないではなくその金額を払うかどうかだからもしかしたら全員半額払うかも知れないし。。。

> という確率分布になります。組み合わせは2の3乗になります。nが大きいとき，この確率分布における80%信頼区間などが欲しいんです。

2^n 通りを全部計算するのではなく，そこからランダムに抽出するということにすればよいでしょう。
つ まり，1〜n人についてn個の一様乱数を発生させ確信度以上なら支払ったとする。この1試行で，視聴料の合計を計算する。これを数万試行行えば，得られる 視聴料の分布が得られるからその分布の20%タイル，80%タイル値を求めたり，x$未満が何%あるかを求めるのは簡単でしょう。
No.01253　Re: 視聴料の合計　　【青木繁伸】　2006/10/07(Sat) 09:45 

> sim <- function(n, a, trial=10000)
+ {
+ 	x <- sapply(1:trial, function(i) sum((runif(n) >  conf)*pay))
+ 	return(sort(x))
+ }
> # n人の回答結果を仮定
> # pay:  0〜50ドル払うとした
> # conf: 支払う確信度 0.25〜0.75 とした
> n <- 100 # 100人を仮定
> pay <- sample(50, n, replace=TRUE)
> conf <- runif(n, min=0.25, max=0.75)
> # 合計支払額が1200$以下の確率を求める, 5万回の試行に基づく
> trial <- 50000
> ans <- sim(n, 1200, trial=trial)
> hist(ans)
> print(paste("[", ans[0.2*trial], ", ", hi=ans[0.8*trial], "]", sep=""))
[1] "[1255, 1490]"
> print(sum(ans <= 1200)/trial)
[1] 0.11082
No.01254　Re: 視聴料の合計　　【水島】　2006/10/07(Sat) 15:07

青木先生ありがとうございました。やはり無作為抽出が妥当ですね。大変参考になりました。これで自信を持って進めていけます。お礼申します。

● 「統計学関連なんでもあり」の過去ログ--- 039 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る