No.00930 Re: サービス時間の平均値推定 【青木繁伸】 2006/08/23(Wed) 17:02
母集団から標本を取り出して,その平均値(標本平均)を求めることを何回も繰り返すことを考えましょう。
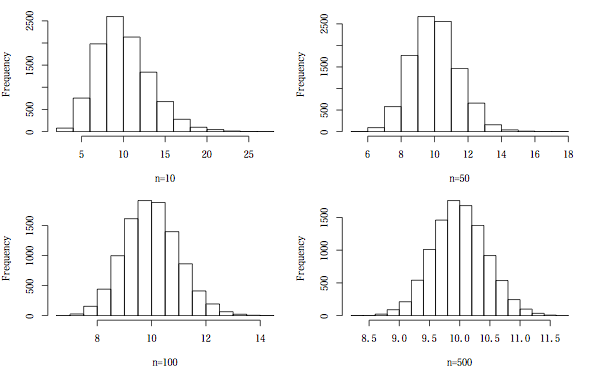
標本平均の分布は,サンプルサイズが小さいうちは母分布の影響を受けますが,サンプルサイズが大きくなるとだんだん正規分布に近くなっていますね。中心極限定理です。
サンプルサイズが十分大きいときには,正規分布によって母平均の推定ができます。
t分布を用いる推定は,正規分布の正確な版ですからO.K.ですね。
しかし,サンプルサイズが小さい(100未満とか??)場合には,前述の通り標本平均の分布が正規分布に全く近似できないので,その母平均の推定値は信頼できないですね。
以下のような,シミュレーションプログラムを書いて確かめることができるでしょう。
n 個の指数乱数を発生させ,t 分布により95%信頼区間を求め,それが母平均を含むかどうかチェックするということを loop 回行い,母平均を含む割合を求める。
これを,n=10, 100, 1000, 10000 の 4 通り行う。
> sim <- function(rate, n=500, loop=10000)
+ {
+ x <- matrix(rexp(n*loop, rate=rate), n, loop)
+ m <- 1/rate
+ count <- 0
+ for (i in 1:loop) {
+ r <- t.test(x[,i])$conf.int
+ if (r[1] < m && m < r[2]) count <- count+1
+ }
+ count/loop
+ }
> sim(0.1, n=10)
[1] 0.9053
> sim(0.1, n=100)
[1] 0.9384
> sim(0.1, n=1000)
[1] 0.9526
> sim(0.1, n=10000)
[1] 0.949
n により,標本平均の分布がどう変わるか以下を参照。