No.00237 Re: 標準偏差と標準誤差 【青木繁伸】 06/06/02(Fri) 14:01
少々長くなりますが,R で実際にシミュレーションしながら(その結果を見ながら)読んでみてください。
まず,最初に標準偏差と標準誤差の意味の確認
正規母集団から標本抽出したとき,平均値±1.96*標準偏差の範囲にデータの95%が含まれると言うこと。
> set.seed(12345) # いつも同じデータが出るようにおまじない正規母集団から標本を取り出したとき,データから母平均の信頼区間を求めるときに使われる
> n <- 50000 # サンプルサイズ
> D <- rnorm(n) # 標準正規母集団から抽出
> M <- mean(D) # 平均値
> SD <- sd(D) # 標準偏差
> z <- qnorm(0.975) # z = 1.96, 上側 2.5% 点
> # 平均値±1.96標準偏差の中にあるデータは何パーセントか
> cat(sum(M-z*SD < D & D < M+z*SD)/n*100, "%\n")
94.958 % # ★★結果★★ ほぼ理論通りでありますね
母平均のわかっている正規母集団から標本を取り出しては信頼区間を求め,その中に母平均が入っているかどうかを調べる。
> set.seed(254383) # いつも同じデータが出るようにおまじないさて,グラフを描くときに「平均値±標準誤差」で描くのは良くないにもかかわらず,(特に医学分野で)よく見られる。
> n <- 100 # サンプルサイズ
> trial <- 50000 # シミュレーション回数
> D <- matrix(rnorm(n*trial), n, trial) # 標準正規乱数
> M <- apply(D, 2, mean) # 各試行での平均値ベクトル
> SE <- apply(D, 2, sd)/sqrt(n) # 各試行での標準誤差ベクトル
> t <- qt(0.975, n-1) # 上側 2.5% 点
> # 平均値±t*標準誤差が母平均を含むのは全試行の何パーセントか
> cat(sum(M-t*SE < 0 & 0 < M+t*SE)/trial*100, "%\n")
94.984 % # ★★結果★★ ほぼ理論通りですね
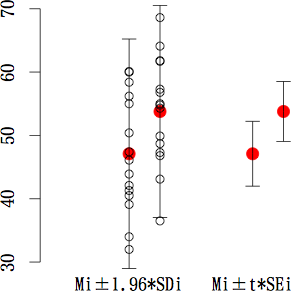
下の方にある図を参照のこと。
好まれる一つの原因。
標準誤差は標準偏差より小さいので,エラーバーが短くて,実験結果がよく見える。
それは間違い。
データがどのように散らばっているかは,平均値と標準偏差に基づかなくてはならない(上の方で述べた)。
> set.seed(987654) # いつも同じデータが出るようにおまじない好まれる理由,その2
> n <- 15 # サンプルサイズ
> D1 <- round(rnorm(n, mean=50, sd=10), 1) # 正規乱数
> D2 <- round(rnorm(n, mean=54.84, sd=10), 1) # 正規乱数
> M1 <- mean(D1) # 平均
> SD1 <- sd(D1) # 標準偏差
> SE1 <- SD1/sqrt(n) # 標準誤差
> M2 <- mean(D2) # 以下同様
> SD2 <- sd(D2)
> SE2 <- SD2/sqrt(n)
> z <- qnorm(0.975) # 上側 2.5% 点
> t <- qt(0.975, n-1) # # 上側 2.5% 点
> print(D1) # 第1群のデータ
[1] 60.0 56.2 47.4 42.1 32.0 41.3 60.1 55.0 43.9 58.4 39.1 34.0 40.5 46.1 50.4
> print(D2) # 第2群のデータ
[1] 55.0 54.3 64.1 49.9 61.7 43.1 68.6 48.7 57.3 56.8 47.3 46.8 36.5 54.8 61.8
> cat(sprintf("n = %i, z = %.5f, t = %.5f\n", n, z, t))
n = 15, z = 1.95996, t = 2.14479
> cat(sprintf("M1 = %.5f, SD1 = %.5f, SE1 = %.5f\n", M1, SD1, SE1))
M1 = 47.10000, SD1 = 9.24415, SE1 = 2.38683
> cat(sprintf("M2 = %.5f, SD2 = %.5f, SE2 = %.5f\n", M2, SD2, SE2))
M2 = 53.78000, SD2 = 8.54285, SE2 = 2.20575
標準誤差で描くと,標準誤差が重なっていないと有意だとわかる。
これは真っ赤なウソ。
実際に上に示したようなデータで,t検定をやってみる(母集団は等分散である)
> t.test(D1, D2, var.equal=TRUE) # 等分散を仮定する平均値の差の検定しかし,下にある図の右側を見ると,標準誤差を表す線は見事に重なっていますね。
Two Sample t-test
data: D1 and D2
t = -2.0554, df = 28, p-value = 0.04927 # ★★結果★★ ぎりぎり有意になるようにデータを作ったのであった
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-13.33726168 -0.02273832
sample estimates:
mean of x mean of y
47.10 53.78
しかも,ほんの少々というわけではない。
な ぜかというと,母平均の信頼区間のときに使われる「t*標準誤差」(図に示されている。しかも,単なる標準誤差ではなく t が掛かっている。)と,二つの平均値の差の信頼区間(これに0が含まれないと言うことが,すなわち母平均に差があるということであるのだが)のときに使わ れる「t*標準誤差」は「違う」(図に表現されていない,tも
異なる),ということである。
大まかに言えば,母平均の信頼区間を求めるときに使われる「t*標準誤差」の1/√2≒
0.7 つまり,図に表現された髭の長さの70%が互いに重なっていなければ有意ということである。
> # 平均値(Mi)と「Mi±fi」の髭を描く関数★★★結論★★★
> draw <- function(p1, M1, M2, f1, f2)
+ {
+ p2 <- p1+0.2
+ points(c(p1, p2), c(M1, M2), pch=19, col="red", cex=1.5)
+ arrows(c(p1, p1, p2, p2), c(M1, M1, M2, M2), c(p1, p1, p2, p2), c(M1+f1, M1-f1, M2+f2, M2-f2), length=0.1, angle=90)
+ }
> # データ点を描く関数
> mark <- function(p1, D1, D2)
+ {
+ p2 <- p1+0.2
+ n <- length(D1)
+ points(rep(c(p1, p2), each=n), c(D1, D2), pch=21)
+ }
> #
> old <- par(xpd=TRUE, cex=1.5, mar=c(3,2,1,0))
> plot(c(0, 1.9), c(min(c(D1, D2)), max(c(D1, D2))), bty="n", type="n", xaxt="n", xlab="", ylim=c(30, 70), ylab="")
> draw(0.5, M1, M2, z*SD1, z*SD2) # 平均値±z*標準偏差のプロット
> mark(0.5, D1, D2) # データ点の描画
> draw(1.3, M1, M2, t*SE1, t*SE2) # 平均値±t*標準誤差のプロット(母平均の信頼区間)
> text(c(0.5, 1.3), min(c(D1, D2))-5, labels=c("Mi±1.96*SDi", "Mi±t*SEi"))
> par(old)
1) 群ごとの平均値を並べて描く場合には,エラーバーは「平均値±1.96*標準偏差」で描くべし。
2) 「範囲内には元のデータの 95% 程が含まれているんだなあ」というように読むべし。
3) 「平均値±標準誤差」で書いても良いけど,その場合は,「範囲内には元のデータの 70% 程が含まれているんだなあ」と読む必要がある。