「統計学関連なんでもあり」の過去ログ--- 038

No.00096　正規分布を利用した問題について　　【波音】　2006/05/19(Fri) 18:27

正規分布を利用した典型的な練習問題だと思うのですが，解答があっているかいささか不安なので間違いを教えてください。

問題：ある大学の出席率はX～N（0.7,0.07^2）の正規分布に従う。このとき5%の学生を落第させるようにするには出席率の下限をどこに設定したらよいか。

解答：1.65=(x-0.7)/0.07 , x=0.7091=70.91(%)となるので出席率が70%に満たない人を落第させるようにすればよい。

それから「ある工場の出荷時の電池寿命は正規分布に従い，平均は3ヶ月，標準偏差は1ヶ月である。無作為に300個を調べたところ平均寿命は2ヶ月と25日であった。何が問題であるか1ヶ月30日として計算せよ。」という問題ですが，（恥ずかしいことに）いってる意味がサッパリ分からんのです。何が問題であるかというのは平均で3ヶ月であるはずが2ヶ月と25日だったのであるから不良品が多いということではないのですか？

No.00097　Re: 正規分布を利用した問題について　　【青木繁伸】　06/05/19(Fri) 18:45

1. 58.48602%
2. P ＝0.001946209（片側）

No.00099　Re: 正規分布を利用した問題について　　【波音】　06/05/19(Fri) 21:08

回答ありがとうございます。

答えを提示していただいてからずっと考えているのですが，どうしても同じ答えにたどり着けません。さわりだけでもやり方を教えていただけないでしょうか。

No.00100　Re: 正規分布を利用した問題について　　【青木繁伸】　06/05/19(Fri) 22:33

答えてしまって良いのかどうかと思いますが，直接の答えでないので良いか（もろ，直接の答えともいえるのだけど）
1. qnorm(0.05, mean=0.7, sd=0.07)
2. pnorm((85-90)/sqrt(30^2/300))

No.00102　Re: 正規分布を利用した問題について　　【波音】　06/05/21(Sun) 16:00

回答ありがとうございます。

z=(85-90)/√30^2/300=-2.886751の値を正規分布表から読み取ると0から2.88までの面積が0.4980と分かるので0.5-0.4980≒0.002となるのですね。

ところで「パーセント点」を辞典で調べると「与えられた確率分布において上側確率が与えられたパーセント値となる点」とありますが，qnorm(0.05, mean=0.7, sd=0.07)で返された値（=0.58）の点はパーセント点といってもよいのでしょうか（図の赤い部分と白い部分の境目の部分）。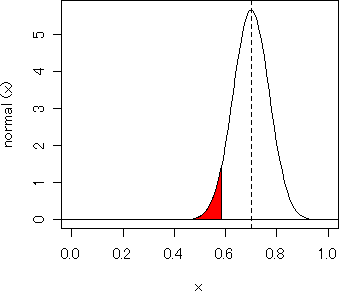

No.00105　Re: 正規分布を利用した問題について　　【青木繁伸】　06/05/21(Sun) 19:10

下からか上からかは，定義しておけばどちらでも良いでしょう。
場合によっては両側確率のパーセント点も定義可能（というか，正規分布や，t分布では両側確率が0.05になるようなパーセント点の方が利用価値が高いとか）。

No.00107　Re: 正規分布を利用した問題について　　【波音】　06/05/21(Sun) 22:44

度々の回答ありがとうございます。
なるほど，定義しておけばどちらの場合で使っても良いのですね。