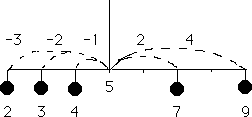
分布の“重心”である。
有効ケース数を $n$,各ケースの測定値を $X_{i}\ ( i = 1,2,\dots ,n )$ とすると,以下の式で定義される。
\[ \bar{X} = \frac{\displaystyle \sum_{i=1}^n X_i}{n} \] 例題:5 つの測定値,2,3,4,7,9 の算術平均値を求めよ。
解答:$\bar{X} = \displaystyle \frac{ 2 + 3 + 4 + 7 + 9 }{5} = 5$
平均値が重心であることは,以下の図を見ればわかる。
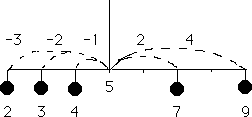
長い竿の 2,3,4,7,9 の位置に同じ重さの分銅が下がっている。これを 5 の位置(重心)でつるすと竿は水平になる。重心の左にある分銅が生み出すモーメントは -3-2-1 = -6,右にある分銅が生み出すモーメントは 2 + 4 = 6 となり,左右のモーメントが打ち消し合うので釣り合いがとれるのである。すなわち,$\displaystyle \sum_{i=1}^n \left (X_i-\bar{X}\right )=0$ である。
度数分布表から平均値を求めるには,各階級の度数を $f_{i}$,その中心点を $X_{i}$,$m$ を階級数として,次式のように定義できる。
\[ \bar{X} = \frac{\displaystyle \sum_{i=1}^m f_i\ X_i}{n} \] 例題:「426 人の女子学生の身長の度数分布が表 1 のようであった。測定精度は無限小であるとして,平均値を求めよ。」
| 階級(単位 cm) | 度数 |
|---|---|
| 140 以上 145 未満 | 4 |
| 145 以上 150 未満 | 19 |
| 150 以上 155 未満 | 86 |
| 155 以上 160 未満 | 177 |
| 160 以上 165 未満 | 105 |
| 165 以上 170 未満 | 33 |
| 170 以上 175 未満 | 2 |
| 合計 | 426 |
解答:「測定精度が無限小」ということは,「140 以上 145 未満」の階級の中心点を 142.5 としてよいということである。
$\bar{X} = ( 4\cdot142.5 + 19\cdot147.5 + 86\cdot152.5 + 177\cdot157.5 + 105\cdot162.5 + 33\cdot167.5 + 2\cdot172.5)\ /\ 426 = 67300\ /\ 426 = 157.98$
演習問題:
「426 人の女子学生の体重の度数分布が表 2 のようであった。」
| 階級(単位 kg) | 度数 |
|---|---|
| 35 以上 40 未満 | 3 |
| 40 以上 45 未満 | 25 |
| 45 以上 50 未満 | 94 |
| 50 以上 55 未満 | 117 |
| 55 以上 60 未満 | 108 |
| 60 以上 65 未満 | 41 |
| 65 以上 70 未満 | 20 |
| 70 以上 75 未満 | 8 |
| 75 以上 80 未満 | 5 |
| 80 以上 85 未満 | 2 |
| 85 以上 90 未満 | 2 |
| 90 以上 95 未満 | 0 |
| 95 以上 100 未満 | 1 |
| 合計 | 426 |
問題1 測定精度が無限小であるとして算術平均値を求めなさい。答えは小数点以下 3 桁目で四捨五入した値を解答欄に記入し,送信ボタンをクリックしなさい。
問題2 測定精度が 0.1 kg であるとして算術平均値を求めなさい。答えは小数点以下 3 桁目で四捨五入した値を解答欄に記入し,送信ボタンをクリックしなさい。
問題3 測定精度をさまざまな値に仮定したとき算術平均値を求め相互に比較し,法則性を見出しなさい。
応用問題: