例題：

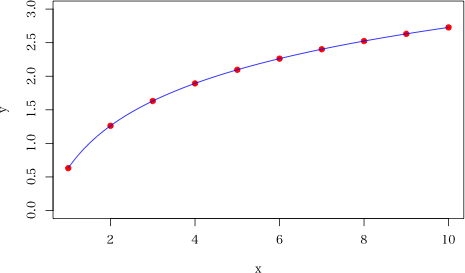
　「表 1 に示すようなデータに曲線をあてはめなさい。」

プログラム：
x <- 1:10
y <- c(0.631, 1.262, 1.631, 1.893, 2.096, 2.262, 2.402, 2.524, 2.631, 2.727)
dat <- data.frame(x=x, y=y)
ans <- lm(y ~ log(x), data=dat) # 両辺の対数をとって，直線回帰式の係数を求める
(p <- ans$coefficients) # 係数
# b^y = a*x の係数に変換する
(a <- exp(p[1]/p[2])) # 元の式の a
(b <- exp(1/p[2]))    # 元の式の b
plot(x, y, pch=19, col="red", ylim=c(0, 3))
x2 <- seq(1, 10, by=0.01)
y2 <- log(a*x2)/log(b)
lines(x2, y2, col="blue")

実行例：
> x <- 1:10
> y <- c(0.631, 1.262, 1.631, 1.893, 2.096, 2.262, 2.402, 2.524, 2.631, 2.727)
> dat <- data.frame(x=x, y=y)
> ans <- lm(y ~ log(x), data=dat)
> p <- ans$coefficients
> (a <- exp(p[1]/p[2]))
(Intercept) 
   2.000198 
> (b <- exp(1/p[2]))
  log(x) 
2.999972 
> plot(x, y, pch=19, col="red")
> x2 <- seq(1, 10, by=0.01)
> y2 <- log(a*x2)/log(b)
> lines(x2, y2, col="blue")
> # quartz(width=500/72, height=350/72)
> x <- 1:10
> y <- c(0.631, 1.262, 1.631, 1.893, 2.096, 2.262, 2.402, 2.524, 2.631, 2.727)
> dat <- data.frame(x=x, y=y)
> ans <- lm(y ~ log(x), data=dat)
> p <- ans$coefficients
> (a <- exp(p[1]/p[2]))
(Intercept) 
   2.000198 
> (b <- exp(1/p[2]))
  log(x) 
2.999972 
> plot(x, y, pch=19, col="red", ylim=c(0, 3))
> x2 <- seq(1, 10, by=0.01)
> y2 <- log(a*x2)/log(b)
> lines(x2, y2, col="blue")