ダミー変数を用いた判別分析による分析の例　　　　　Last modified: May 16, 2002

　まず最初に，分析に使用するデータを準備する。各アイテム変数を，「その変数が持つカテゴリー数 − １」個のダミー変数に変換する（表 2 参照）。

　例えば，あるアイテム変数が 3 個のカテゴリーを持つときは 2 個のダミー変数をあてる。アイテム変数の値が 1 のときは，2 個のダミー変数は 0, 0 とし，2 のときは 1, 0 とし，3 のときは 0, 1 とする。

表 1．数量化 II 類による分析に使うデータ例
ケース番号 $x_{1}$ $x_{2}$ 　群　
1 1 1 1
2 1 2 1
3 1 2 1
4 1 2 1
5 1 3 1
6 2 1 1
7 2 1 1
8 2 1 2
9 2 2 2
10 2 3 1
11 2 3 2
12 3 1 2
13 3 2 2
14 3 3 2
15 3 3 2
 　　　　　
表 2．カテゴリー変数をダミー変数に展開したデータ
ケース番号 $d_{11}$ $d_{12}$ $d_{21}$ $d_{22}$ 　群　
1 0 0 0 0 1
2 0 0 1 0 1
3 0 0 1 0 1
4 0 0 1 0 1
5 0 0 0 1 1
6 1 0 0 0 1
7 1 0 0 0 1
8 1 0 0 0 2
9 1 0 1 0 2
10 1 0 0 1 1
11 1 0 0 1 2
12 0 1 0 0 2
13 0 1 1 0 2
14 0 1 0 1 2
15 0 1 0 1 2

***** 判別係数 *****
判別係数 　　標準化判別係数
$d_{11}$　　 -5.52441 -2.70640　　
$d_{12}$　　 -9.87342 -4.36619　　
$d_{21}$　　 -2.20976 -1.04169　　
$d_{22}$　　 -1.01085 -0.47652　　
定数項　 6.11358

判別係数の解釈は以下のようになる。
元のアイテム変数 $x_{i}$ は，2 個のダミー変数 $d_{i1}$ と $d_{i2}$ を使って表現されている（$i = 1, 2$）。それぞれのダミー変数に対する判別係数を $b_{i1}$ ，$b_{i2}$ とすると，判別値は $\hat{y} = d_{11}\cdot b_{11} + d_{12}\cdot b_{12} + d_{21}\cdot b_{21} + d_{22}\cdot b_{22} + 定数項$ であらわされる。

$x_{1}$ が 1 という値を取るときは，$d_{11} = 0$，$d_{12} = 0$ であるから，判別値に寄与する値は $0\cdot 6.74375 + 0\cdot 17.225 = 0 $である。
$x_{1}$ が 2 という値を取るときは，$d_{11} = 1$，$d_{12} = 0$ であるから，判別値に寄与する値は $1\cdot (-5.52441) + 0\cdot (-9.87342) = -5.52441$ である。すなわち，この場合は $x_{1} = 1$ の場合に比べて判別値は $5.52441$ 小さくなる。
$x_{1}$ が 3 という値を取るときは，$d_{11} = 0$，$d_{12} = 1$ であるから，判別値に寄与する値は $0\cdot (-5.52441) + 1\cdot (-9.87342) = -9.87342$ である。すなわち，この場合は $x_{1} = 1$ の場合に比べて判別値は $9.87342$ 小さくなる。

標準化判別係数の大きさからいうと，予測をするために最も重要なのは $d_{12}$ であり，次いで $d_{11}$ である（これらに対する $P$ 値が小さいので，これらの係数が 0 でないといってよいことがわかる）。$d_{22}$ ，$d_{21}$ はそれらに比べて予測という観点からはあまり重要ではないことがわかる。

***** 各ケースの判別結果 *****
ケース 　実際の群　 判別された群 　　二乗距離 1 　　二乗距離 2 　　　判別値
1 1 1 　　 4.31(0.366) 16.54(0.002) 6.11358
2 1 1 　　 1.77(0.778) 9.58(0.048) 3.90382
3 1 1 　　 1.77(0.778) 9.58(0.048) 3.90382
4 1 1 　　 1.77(0.778) 9.58(0.048) 3.90382
5 1 1 　　 3.99(0.407) 14.20(0.007) 5.10274
6 1 1 　　 3.32(0.505) 4.50(0.342) 0.58917
7 1 1 　　 3.32(0.505) 4.50(0.342) 0.58917
8 2 1 #　 3.32(0.505) 4.50(0.342) 0.58917
9 2 2 　　 7.93(0.094) 4.69(0.321) -1.62059
10 1 2 #　 5.17(0.270) 4.33(0.364) -0.42168
11 2 2 　　 5.17(0.270) 4.33(0.364) -0.42168
12 2 2 　　 11.47(0.022) 3.95(0.413) -3.75983
13 2 2 　　 16.17(0.003) 4.23(0.376) -5.96960
14 2 2 　　 11.97(0.018) 2.43(0.657) -4.77068
15 2 2 　　 11.97(0.018) 2.43(0.657) -4.77068
 　　　 判別値は数量化 I 類による結果比例する。

結局，判別係数の値とノーマライズドカテゴリースコアの値は異なるように見えるが，定数項を含めた調整の後では全く等価な判別値を与える重みであることが分かる。

***** 判別結果総括表 *****
判別された群
実際の群 群 1 群 2 合計
群 1 7 1 8
% (87.5) (12.5) (100.0)
群 2 1 6 7
% 　(14.3) 　(85.7) 　(100.0)
正判別率=86.67%
 　　　 第 1 群の 8 例中 7 例，第 2 群の 7 例中 6 例が正しく判別できている。正判別率は正しく判別された数（7+6）を全体の数 15 で割った割合として求めてある。

数量化 II 類の結果と全く同じである。

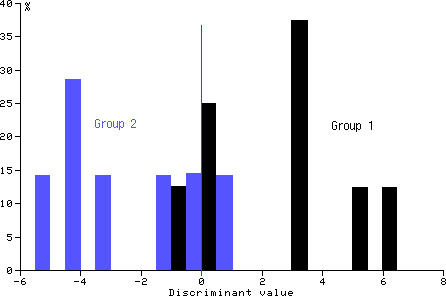
***** 二群の判別図 *****

figure

・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI