ダミー変数を用いた重回帰分析による分析の例　　　　　Last modified: May 16, 2002

　まず最初に，分析に使用するデータを準備する。各アイテム変数を，「その変数が持つカテゴリー数 − １」個のダミー変数に変換する（表 2 参照）。

　例えば，あるアイテム変数が 3 個のカテゴリーを持つときは 2 個のダミー変数をあてる。アイテム変数の値が 1 のときは，2 個のダミー変数は 0, 0 とし，2 のときは 1, 0 とし，3 のときは 0, 1 とする。

表 1．数量化 I 類による分析に使うデータ例
ケース番号 x_{1} x_{2} y
1 1 1 9.3
2 1 2 7.6
3 1 2 11.9
4 1 2 12.4
5 1 3 14.7
6 2 1 17.7
7 2 1 10.4
8 2 1 19.8
9 2 2 21.1
10 2 3 15.0
11 2 3 20.5
12 3 1 23.6
13 3 2 27.4
14 3 3 31.2
15 3 3 33.4
 　　　　　
表 2．カテゴリー変数をダミー変数に展開したデータ
ケース番号 d_{11} d_{12} d_{21} d_{22} y
1 0 0 0 0 9.3
2 0 0 1 0 7.6
3 0 0 1 0 11.9
4 0 0 1 0 12.4
5 0 0 0 1 14.7
6 1 0 0 0 17.7
7 1 0 0 0 10.4
8 1 0 0 0 19.8
9 1 0 1 0 21.1
10 1 0 0 1 15.0
11 1 0 0 1 20.5
12 0 1 0 0 23.6
13 0 1 1 0 27.4
14 0 1 0 1 31.2
15 0 1 0 1 33.4

***** 分析に用いた変数の基礎統計量 *****
　 　　　　平均値　　 　　　不偏分散　　 　　　　標準偏差　
y 18.400000000 62.712857143 7.9191449755
d_{11} 0.400000000 0.257142857 0.5070925528
d_{12} 0.266666667 0.209523810 0.4577377082
d_{21} 0.333333333 0.238095238 0.4879500365
d_{22} 0.333333333 0.238095238 0.4879500365

***** 相関係数行列 *****
y　　 1.00000
d_{11}　　 　-0.10494 　1.00000
d_{12}　　 　0.82761 　-0.49237 　1.00000
d_{21}　　 　-0.21443 　-0.28868 　-0.10660 　1.00000
d_{22}　　 　0.42146 　0.00000 　0.21320 　-0.50000 　1.00000
y d_{11} d_{12} d_{21} d_{22}

***** 重回帰式 *****
　 　　偏回帰係数 　　標準誤差 　　　　　ｔ値 　　　　Ｐ値 　標準化偏回帰係数
d_{11}　 6.743750 2.266673 2.9751749 0.01392 0.4318276　　
d_{12}　 17.22500 2.423176 7.1084399 0.00003 0.9956292　　
d_{21}　 2.617500 2.349356 1.1141350 0.29128 0.1612812　　
d_{22}　 4.703750 2.214258 2.1243010 0.05959 0.2898286　　
定数項 8.668750 2.266673 3.8244371 0.00335
ｔ値の自由度は $10$

偏回帰係数の解釈は以下のようになる。
元のアイテム変数 $x_{i}$ は，2 個のダミー変数 $d_{i1}$ と $d_{i2}$ を使って表現されている（$i = 1, 2$）。それぞれのダミー変数に対する偏回帰係数を $b_{i1}$ ，$b_{i2}$ とすると，予測値は $\hat{y} = d_{11}\cdot b_{11} + d_{12}\cdot b_{12} + d_{21}\cdot b_{21} + d_{22}\cdot b_{22} + 定数項$ であらわされる。

$x_{1}$ が 1 という値を取るときは，$d_{11} = 0，d_{12} = 0$ であるから，予測値に寄与する値は $0\cdot 6.74375 + 0\cdot 17.225 = 0 $である。
$x_{1}$ が 2 という値を取るときは，$d_{11} = 1，d_{12} = 0$ であるから，予測値に寄与する値は $1\cdot 6.74375 + 0\cdot 17.225 = 6.74375$ である。すなわち，この場合は $x_{1} = 1$ の場合に比べて予測値は $6.74375$ 大きくなる。
$x_{1}$ が 3 という値を取るときは，$d_{11} = 0，d_{12} = 1$ であるから，予測値に寄与する値は $0\cdot 6.74375 + 1\cdot 17.225 = 17.225$ である。すなわち，この場合は $x_{1} = 1$ の場合に比べて予測値は $17.225$ 大きくなる。

標準化偏回帰係数の大きさからいうと，予測をするために最も重要なのは $d_{12}$ であり，次いで $d_{11}$ である（これらに対する $P$ 値が小さいので，これらの係数が 0 でないといってよいことがわかる）。$d_{22}$ ，$d_{21}$ はそれらに比べて予測という観点からはあまり重要ではないことがわかる（これらに対する $P$ 値が大きいので，これらの係数は 0 でないととはいえないということがわかる）。

***** 分散分析表 *****
要因 　　　平方和 　　自由度 　　平均平方 　　　　Ｆ値 　　　Ｐ値
回帰 760.5444 4 190.1361 16.19067 0.00023
残差 117.4356 10 11.74356
全体 877.9800 14
　　　 $P$ 値が 小さいので（例えば $5\%$ の有意水準で検定すると），この重回帰式により十分予測できるといえる。

重相関係数 = 0.93072
決定係数（重相関係数の二乗） = 0.86624
自由度調整済み重相関係数の二乗 = 0.81274
 　　　 重相関係数，決定係数の値は数量化 I 類による結果と全く同じになる

***** 従属変数の観察値，予測値および標準化残差 *****
ケース 　　観察値 　　　予測値 　　　　残差 　標準化残差
1 9.3 8.66875 0.63125 0.24038
2 7.6 11.28625 -3.68625 -1.23779
3 11.9 11.28625 0.61375 0.20609
4 12.4 11.28625 1.11375 0.37398
5 14.7 13.37250 1.32750 0.50253
6 17.7 15.41250 2.28750 0.76458
7 10.4 15.41250 -5.01250 -1.67538
8 19.8 15.41250 4.38750 1.46648
9 21.1 18.03000 3.07000 1.15313
10 15.0 20.11625 -5.11625 -1.78544
11 20.5 20.11625 0.38375 0.13392
12 23.6 25.89375 -2.29375 -0.87346
13 27.4 28.51125 -1.11125 -0.43006
14 31.2 30.59750 0.60250 0.21203
15 33.4 30.59750 2.80250 0.98626
 　　　 予測値は数量化 I 類による結果と全く同じになる。

結局，偏回帰係数の値とノーマライズドカテゴリースコアの値は異なるように見えるが，定数項を含めた調整の後では全く同じ予測値を与える重みであることが分かる。

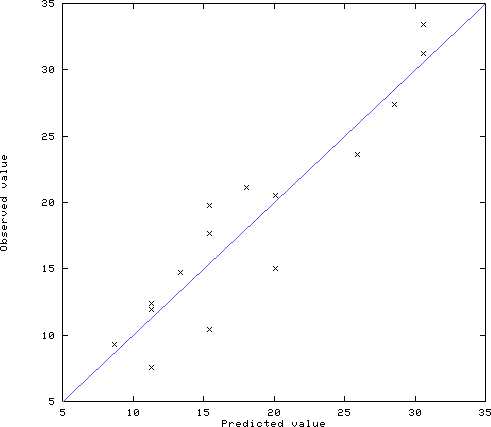
***** 予測値と観察値のプロット *****
figure 　　　 予測値と観察値はほぼ傾き１の直線の近辺にあり，予測が比較的うまくいっている（数量化 I 類の結果と全く同じ図である）。

・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI