$x_{1} , x_{2}$ に与えられたカテゴリースコアに基づいて計算された相関係数行列

***** 相関係数行列 *****

y　　 1.00000 x_{1}　　 0.89653 　1.00000 x_{2}　　 0.34814 　0.11123 　1.00000 y x_{1} x_{2}

従属変数 $y$ と最も相関の高いのは $x_{1}$ であることがわかる。 $x_{1}$ と $x_{2}$ の相関は低い。

正規化されたカテゴリースコア
偏相関係数は各アイテム変数と従属変数との他のアイテム変数の影響を除いた相関

***** ノーマライズド スコア *****

アイテム-カテゴリー 　カテゴリースコア 　偏相関係数 x_{1} - 1　　　　 -7.290833　　 0.92076 - 2　　　　 -0.547083　　 - 3　　　　 9.934167　　 x_{2} - 1　　　　 -2.440417　　 0.56428 - 2　　　　 0.177083　　 - 3　　　　 2.263333　　 定数項　　　　 18.40000

ここでもやはり従属変数 $y$ と最も相関の高いのは $x_{1}$ であることがわかる。 $x_{1}$ に与えられたカテゴリースコアはカテゴリー間で不等間隔であることがわかる。 $x_{2}$ に与えられたカテゴリースコアはカテゴリー間でほぼ等間隔であることがわかる。

予測がうまくできるかどうかの指標

重相関係数 = 0.93072　　決定係数（重相関係数の二乗）= 0.86624

決定係数が 1 に近いほど予測がうまくいっていることを表す。

***** 従属変数の観察値と予測値および残差 *****

ケース 　観察値 　　　予測値 　　　　残差 1 9.3 8.66875 0.63125 2 7.6 11.28625 -3.68625 3 11.9 11.28625 0.61375 4 12.4 11.28625 1.11375 5 14.7 13.37250 1.32750 6 17.7 15.41250 2.28750 7 10.4 15.41250 -5.01250 8 19.8 15.41250 4.38750 9 21.1 18.03000 3.07000 10 15.0 20.11625 -5.11625 11 20.5 20.11625 0.38375 12 23.6 25.89375 -2.29375 13 27.4 28.51125 -1.11125 14 31.2 30.59750 0.60250 15 33.4 30.59750 2.80250

例えば，8 番目のケースの従属変数 $y$ の実測値は 19.8，$x_{1} = 2，x_{2} = 1$ である。 予測値は，$x_{1}$ のカテゴリー 2 に対応するカテゴリースコア $-$0.5470833 と $x_{2}$ のカテゴリー 1 に対応するカテゴリースコア $-$2.440417 を加え，更に定数項 18.4 を加えることにより 15.4125 となる。

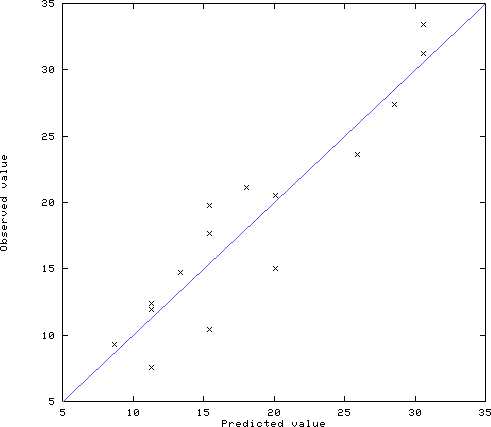
***** 予測値と観察値のプロット *****

予測値と観察値はほぼ傾き１の直線の近辺にあり，予測が比較的うまくいっている