 $P$ の余事象(水色の部分) |
|---|
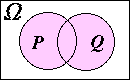 $P$ と $Q$ の和事象(紫色の部分) |
|---|
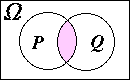 P と $Q$ の積事象(紫色の部分) |
|---|
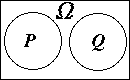 排反事象($P$ と $Q$ が排反) |
|---|
カードを引いたり,サイコロを投げたりという試みは何回も繰り返すことができ,その結果は偶然のみに支配されるとみなせる。
このような試みを 試行 といい,試行の結果として考えられる事柄を 事象 という。
特に,1 回の試行で $n$ 個の事象 $\omega_1, \omega_2, \dots, \omega_n$ のうちのどれかが必ず起こり,しかも 2 つ以上の事象が同時に起こることはないとき,これらの事象 $\omega_1, \omega_2, \dots, \omega_n$ を 根元事象 という。
根元事象全体の集合を 標本空間 といい,$\Omega$( オメガ )で表すことにしよう。
一般の事象は,特定の条件を満たす根元事象の集合,すなわち $\Omega$ の部分集合とみなされる。
サイコロの出る目の標本空間は,
であり,奇数の目が出るという事象を $A$,素数の目が出るという事象を $B$ とすると,それぞれ,
と表される。
これらの集合はいずれも標本空間 $\Omega$ の部分集合である。事象とそれを表す集合とを特に区別しないで,同じ記号 $A$,$B$ などで表す。
 $P$ の余事象(水色の部分) |
|---|
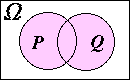 $P$ と $Q$ の和事象(紫色の部分) |
|---|
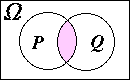 P と $Q$ の積事象(紫色の部分) |
|---|
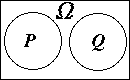 排反事象($P$ と $Q$ が排反) |
|---|
演習問題:
応用問題: