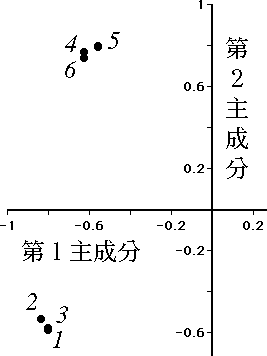
 図 1.回転前の因子負荷量 |
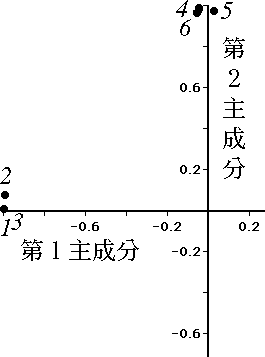 図 2.回転後の因子負荷量 |
|---|
主成分の解釈を容易にするために主成分軸の回転を行うことができる。
 図 1.回転前の因子負荷量 |
 図 2.回転後の因子負荷量 |
|---|
主成分軸の回転は以下のように行う。
\[ \mathbf{B} = \mathbf{A}\mathbf{T} \]
\[ h_j^2 = \sum_{k=1}^m b_{jk}^2 \] で因子負荷量を基準化したものを
\[ q_{ij} = \frac{b_{ij}}{h_j} \] とする。
\[ c = \sum_{k=1}^m \sum_{j=1}^p q_{jk}^4 - \frac{w}{p} \sum_{k=1}^m \left ( \sum_{j=1}^p q_{jk}^2 \right )^2 \] を最大にすることができる。
$w$ のとる値によって特性の異なる因子負荷量行列が得られる。
\[ w = \left \{ \begin{align*} 1, & バリマックス回転 \\[5pt] 0.5, & バイコーティマックス回転 \\[5pt] 0, & コーティマックス回転 \\[5pt] \displaystyle \frac{m}{2}, & エクィマックス回転 \end{align*} \right . \]
\[ \left \{ \begin{array}{l} t_{kk} = \cos \theta \\[5pt] t_{kk'} = -\sin \theta \\[5pt] t_{k'k} = \sin \theta \\[5pt] t_{k'k'} = \cos \theta \tag{1} \end{array} \right . \] ただし,$\theta$ は( 2 )式を満たすものとする。 \[ \left \{ \begin{array}{l} \tan 4\ \theta = \displaystyle \frac{D-\displaystyle \frac{2\;A\;B}{p}}{C-\displaystyle \frac{A^2-B^2}{p}} \\[5pt] \left ( D-\displaystyle \frac{2\;A\;B}{p} \right ) \sin 4\ \theta > 0 \tag{2} \end{array} \right . \] ここで,$r_{j} = \displaystyle \frac{a_{jk}}{h_{j}}$,$s_{j} = \displaystyle \frac{a_{jk'}}{h_{j}}$ として,
\[ \left \{ \begin{align*} A &= \displaystyle \sum_{j=1}^p (r_j^2-s_j^2) \\[5pt] B &= 2\displaystyle \sum_{j=1}^p r_j\ s_j \\[5pt] C &= \displaystyle \sum_{j=1}^p (r_j^4+s_j^4-6r_j^2\ s_j^2) \\[5pt] D &= 4\displaystyle \sum_{j=1}^p r_j\ s_j\ (r_j^2-s_j^2) \end{align*} \right . \]
演習問題:
応用問題: