計算された検定統計量を $S_{0}$ とし， $S_{0}$ はある分布に従うことがわかっているとする。

　このとき，有意確率 $P$ は，以下のように定義される。

• 片側検定のとき（図 1，2 参照）

  $P = P_{U} = \Pr\{ S \geqq S_{0} \}$ または

  $P = P_{L} = \Pr\{ S \leqq S_{0}' \}$

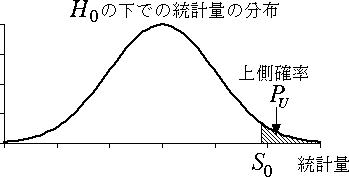  図 1．片側検定の場合の有意確率

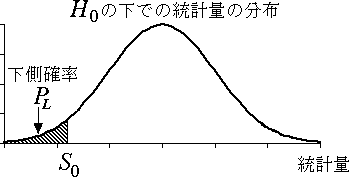  図 2．片側検定の場合の有意確率

• 両側検定のとき（図 3 参照）

  $P = P_{U} + P_{L} = \Pr\{ S \geqq S_{0} \}+ \Pr\{ S \leqq S_{0}' \}$

  統計量の分布が原点対称の場合には，$S_{0}' = - S_{0}$ なので，

  $P = \Pr\{|\,S\,|\geqq|\,S_{0}\,|\}$ または

  $P = 2 \times \Pr\{ S \geqq|\,S_{0}\,|\}$

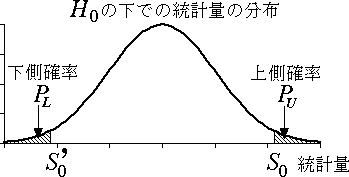  図 3．両側検定の場合の有意確率

　有意確率を求めるには，統計数値表を参照することもできるが，正確な値を求めるにはコンピュータを用いる方がよい。

　★ 統計学上の分布関数に関する計算

演習問題：

問題1　標準正規分布において，標準得点が $1.96$ 以上になる確率を求めなさい。答えは小数点以下 4 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題2　自由度が 3 の$\chi^2$ 分布において，$\chi^2$ 値が $3.5$ 以上になる確率を求めなさい。答えは小数点以下 4 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題3　自由度が 10 の $t$ 分布において，$|\,t\,|\geqq 1.5$ 以上になる確率を求めなさい。答えは小数点以下 4 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

問題4　自由度が 10 の $t$ 分布において，両側確率が $0.05$ になるときの値 $t_0\ (\Pr\{|\,t\,|\geqq t_0 \})$ を求めなさい。答えは小数点以下 4 桁目で四捨五入した値を解答欄に記入し，送信ボタンをクリックしなさい。

解答欄：　　　　

応用問題：