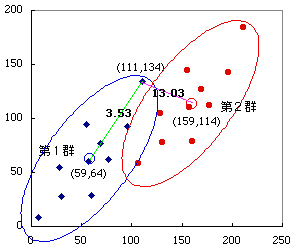
図 2. マハラノビスの平方距離とユークリッド距離の関係
マハラノビスの平方距離に基づき,距離の近い群に判別するということを,架空例で見てみよう。
2 群のデータを考える。各群 10 組の2 変数データとする。データは表 1 の通り。
|
|
> data1 X1 X2 1 7 8 2 30 28 3 60 29 4 28 55 5 57 60 6 77 62 7 69 77 8 55 94 9 96 93 10 111 134 > ( m1 <- colMeans(data1) ) # 第 1 群の平均値 群 X1 X2 1 59 64 > data2 X1 X2 1 107 58 2 130 78 3 160 79 4 128 105 5 157 110 6 177 112 7 169 127 8 155 144 9 196 143 10 211 184 > ( m2 <- colMeans(data2) ) # 第 2 群の平均値 X1 X2 159 114
分散・共分散行列および,その逆行列を計算する。第 1 群と第 2 群の分散・共分散行列は全く等しいことに注意。
> ( n1 <- nrow(data1) ) # 第 1 群のサンプルサイズ [1] 10 > ( n2 <- nrow(data2) ) # 第 2 群のサンプルサイズ [1] 10 > ( S1 >- var(data1)*(n1-1) ) # 第 1 群の変動・共変動行列 X1 X2 X1 9024 8895 X2 8895 12568 > ( S2 >- var(data2)*(n2-1) ) # 第 2 群の変動・共変動行列 X1 X2 X1 9024 8895 X2 8895 12568 > ( V <- (S1+S2)/(n1+n2-2) ) # 二群をプールした分散・共分散行列 X1 X2 X1 1002.6667 988.3333 X2 988.3333 1396.4444 > ( inv.S <- solve(V) ) # 二群をプールした分散・共分散行列の逆行列 X1 X2 X1 0.003298437 -0.002334468 X2 -0.002334468 0.002368324
マハラノビスの平方距離は,分散共分散行列の逆行列を用いて計算する。
第 1 群の 10 番目の例 (111, 134) について,各群の重心までマハラノビスの平方距離の計算例を以下に示す。
(111, 134) から (59, 64) への距離
\[
\begin{align*}
&(111, 134) - (59, 64) = (52, 70)\\[5pt]
&(52\ \ 70)\left (
\begin{array}{rr}
0.003298437 & -0.002334468 \\
-0.002334468 & 0.002368324
\end{array}
\right )
\left (
\begin{array}{r}
52 \\
70
\end{array}
\right ) \\[5pt]
&=3.528831972
\end{align*}
\]
> ( diff1 <- c(111, 134)-m1 ) X1 X2 52 70 > ( dist2 <- diff1 %*% inv.S %*% diff1 ) [,1] [1,] 3.528832
(111, 134) から (159, 114) への距離
\[
\begin{align*}
&(111, 134) - (159, 114) = (-48, 20)\\[5pt]
&(-48\ \ 20)\left (
\begin{array}{rr}
0.003298437 & -0.002334468 \\
-0.002334468 & 0.002368324
\end{array}
\right )
\left (
\begin{array}{r}
-48 \\
20
\end{array}
\right ) \\[5pt]
&=13.02910706
\end{align*}
\]
> ( diff2 <- c(111, 134)-m2 ) X1 X2 -48 20 > ( dist2 <- diff2 %*% inv.S %*% diff2 ) [,1] [1,] 13.02911
この結果を図 2 に示す。
 図 2. マハラノビスの平方距離とユークリッド距離の関係 |
ユークリッド距離では,緑で描いた線分は紫で描いた線分より長い(距離が長い)。しかし,第 1 群の重心までのマハラノビス距離は 3.53,第 2 群の重心までのマハラノビス距離は 13.03 である。その理由は,各群のデータは楕円で示したような二次元(正規分布)をしているので,ユークリッド距離的に楕円の長軸方向と短軸方向へ同じだけ離れた点までのマハラノビス距離は異なるのである(短軸方向の距離の方が長い)。
それぞれのデータが各グループに属する確率は,マハラノビスの平方距離が自由度 $p$ のカイ二乗分布に従うことに基づいて計算できる($p$ は判別分析に用いた変数の個数)。
第 1 群の 10 番目の例 (111, 134) は,第 1 群までの平方距離が 3.528832,第 2 群までの平方距離が 13.02911 であり,$p = 2$ であるから,各群に属する確率はそれぞれ約 0.17128,0.00148 となる。
> ( p <- ncol(data1) ) # 変数の個数 [1] 2 > ( p1 <- pchisq(dist1, 2, lower.tail=FALSE) ) [,1] [1,] 0.1712868 > ( p2 <- pchisq(dist2, 2, lower.tail=FALSE) ) [,1] [1,] 0.001481717
このデータを判別分析した結果例を以下に示す。
★ 平均値
全体 第1群 第2群
20ケース 10ケース 10ケース
2 Var002 109.0000 59.00000 159.0000
3 Var003 89.00000 64.00000 114.0000
★ 判別関数
判別係数 標準化判別係数
2 Var002 -0.21312 -12.43133
3 Var003 0.11503 4.99000
定数項 12.99238
★ 各ケースの判別結果
ケース R P 平方距離1 平方距離2 判別値
1 1 1 2.75(0.253) 27.59(0.000) 12.42079
2 1 1 0.97(0.616) 20.61(0.000) 9.81963
3 1 1 3.07(0.216) 10.15(0.006) 3.54106
4 1 1 2.06(0.357) 28.76(0.000) 13.35170
5 1 1 0.01(0.993) 15.51(0.000) 7.74637
6 1 1 1.25(0.536) 8.67(0.013) 3.71402
7 1 1 0.12(0.940) 14.41(0.001) 7.14444
8 1 1 2.74(0.254) 26.91(0.000) 12.08365
9 1 1 1.50(0.473) 7.96(0.019) 3.23069
10 1 1 3.53(0.171) 13.03(0.001) 4.75014 図 1 の計算例に示したもの
11 2 2 9.03(0.011) 2.75(0.253) -3.13971
12 2 2 12.45(0.002) 0.97(0.616) -5.74086
13 2 2 27.11(0.000) 3.07(0.216) -12.01944
14 2 2 6.48(0.039) 2.06(0.357) -2.20880
15 2 2 15.64(0.000) 0.01(0.993) -7.81413
16 2 2 24.94(0.000) 1.25(0.536) -11.84647
17 2 2 16.96(0.000) 0.12(0.940) -8.41605
18 2 2 9.70(0.008) 2.74(0.254) -3.47685
19 2 2 26.16(0.000) 1.50(0.473) -12.32981
20 2 2 25.15(0.000) 3.53(0.171) -10.81036
注:‘平方距離'は各群の重心までのマハラノビスの平方距離
カッコ内は各群に属する確率
★ 判別結果
判別された群
実際の群 第1群 第2群 合計
第1群 10 0 10
% (100.0) ( 0.0) (100.0)
第2群 0 10 10
% ( 0.0) (100.0) (100.0)
正判別率 ・・・ 100.00%
