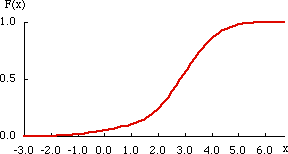
 図 1.分布関数 $F( x )$ |
|---|
分布関数 $F ( x )$ は,次のような基本的条件を満たす関数である。
すなわち,$F ( x )$ は単調非減少関数である。
すなわち,$F ( x )$ は $x \rightarrow \pm \infty$ において極限を持つこと,および,$F ( x )$ は非負であること。
 図 1.分布関数 $F( x )$ |
|---|
以上のような各性質を持つ関数のうちで,実用的な価値を持つものは次の 2 種である。
至るところ連続で,$F'( x ) = f ( x )$ が存在し,かつそれが有限個の点以外では,全ての点で連続である。
$f ( x )$ を $F$ の密度関数という。
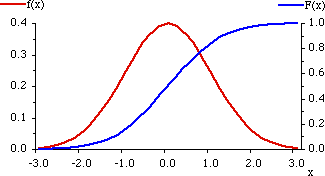 図 2.連続変数の分布関数と密度関数 |
|---|
不連続点 $x_{i}$ で,それぞれ $p_{i}$ ずつ飛躍する。
つまり,$p_{i} = F ( x_{i} ) - F ( x_{i} - 0 )$ である。
確率関数は $f ( x_{i} ) = p_{i}$ である。
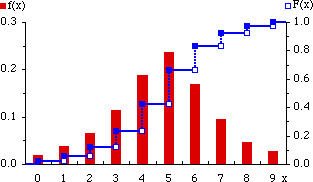 図 3.離散変数の分布関数と確率関数 |
|---|
演習問題:
応用問題: