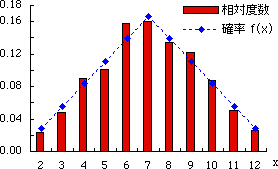
 図 1.相対度数と確率 |
|---|
2 個のサイコロを1000 回振って毎回の出た目の和を記録するという実験を行った結果を,表 1 の左半分に示す。
理論的に考察すると,目の和が最小であるのは,両方のサイコロが共に 1 の目が出たときであり,これは 1 / 36 の確率であることが分かる。目の和が 3 になるのは, ( 1, 2 ) という出方と ( 2, 1 ) という出方の 2 通りであり 2 / 36 となる。これをまとめると表 1 の右半分になる。
| 和 $x_{i}$ | 度数 | 相対度数 | 累積相対度数 | 確率 $f(x_{i})$ | 分布関数 $F(x_{i})$ |
|---|---|---|---|---|---|
| 2 | 23 | 0.023 | 0.023 | 1/36=0.028 | 1/36=0.028 |
| 3 | 48 | 0.048 | 0.071 | 2/36=0.056 | 3/36=0.083 |
| 4 | 90 | 0.090 | 0.161 | 3/36=0.083 | 6/36=0.167 |
| 5 | 101 | 0.101 | 0.262 | 4/36=0.111 | 10/36=0.278 |
| 6 | 158 | 0.158 | 0.420 | 5/36=0.139 | 15/36=0.417 |
| 7 | 160 | 0.160 | 0.580 | 6/36=0.167 | 21/36=0.583 |
| 8 | 135 | 0.135 | 0.715 | 5/36=0.139 | 26/36=0.722 |
| 9 | 122 | 0.122 | 0.837 | 4/36=0.111 | 30/36=0.833 |
| 10 | 87 | 0.087 | 0.924 | 3/36=0.083 | 33/36=0.917 |
| 11 | 50 | 0.050 | 0.974 | 2/36=0.056 | 35/36=0.972 |
| 12 | 26 | 0.026 | 1.000 | 1/36=0.028 | 36/36=1.000 |
| 合計 | 1000 | 1.000 | 1.000 |
表 1 において,“相対度数”と“確率”の列,“累積相対度数”と“分布関数”の列の数値がかなり似ていることがわかる。
累積相対度数は経験的分布関数であり,その極限的なものが理論的分布関数 $F ( x_{i} )$ である(略して分布関数あるいは確率分布と呼ぶ。)。
 図 1.相対度数と確率 |
|---|
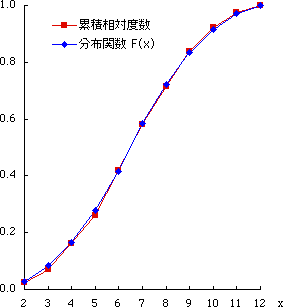 図 2.累積相対度数と分布関数 |
|---|
演習問題:
サイコロを振る実験をしてみなさい。
参考:インターネットでサイコロを振るページ
応用問題: