実例をもって示してゆこうと思う。よって，完成するまでには時間がかかる。適切な実例があれば報告していただければ幸いである。

直前のページへ戻る

　正確なP値は，標本サイズが無限大になると数学的には漸近的なP値に近づく。
　しかし，この特性は特定のデータセットにおいて漸近的なP値の精度を保証する上ではあまり実際的な価値を持たない。

　漸近的な方法がうまく機能しないのは以下のような場合である。

• 小規模なデータセット

  　全例数が少ない場合である。「小標本データのまとめかた」などという本があったように，大標本論が適用できない場合には注意が必要である。
  

• 同値を含むデータセット

  　カテゴリーデータは必然的に同値が多くなる。ノンパラメトリック検定は同値について適切な方法を用意しているが，それさえも解説していない教科書が多すぎる。
  

• 大きいがアンバランスなデータセット

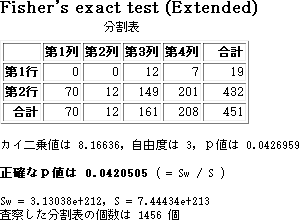
  　公衆衛生関係の学会誌に載っていた実例である。論文著者は以下の分割表（2 群の分布の差）に対してカイ二乗検定を行っている。

  
  　二群の比較をおこなう各群のケース数が 19 例と 432 例であり，かなり異なっている。論文著者は通常のカイ二乗検定を行って「有意である」としているが，期待値が 1 未満のセルがあるので，カイ二乗検定が不適切である可能性がある。しかし，Exact test によって得られた P 値はほとんど同じであり，検定結果は変わらなかった。
  　結論は変わらなかったが，このデータにおいて列カテゴリーには順序があるので，マン・ホイットニーの U 検定を使うのがよいであろう。

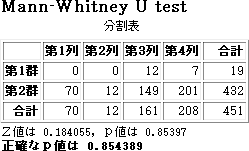  　Ｐ値はとんでもない大きな値になるが，漸近的な P 値も，正確な P 値もほとんど同じになる。結局，このデータセットからは，2 群間に差はないということである。

  　なお，この例では（分割表の検定ではほとんどいつもそうではあるが）同値が多いのも漸近的な方法がうまく機能しない理由となっているのである。
  

• 疎なデータセット

  　小規模なデータセットであるにもかかわらず，カテゴリー数が多いと観察のないセルが多くなる。漸近的な P 値はほとんど機能しなくなってしまう。