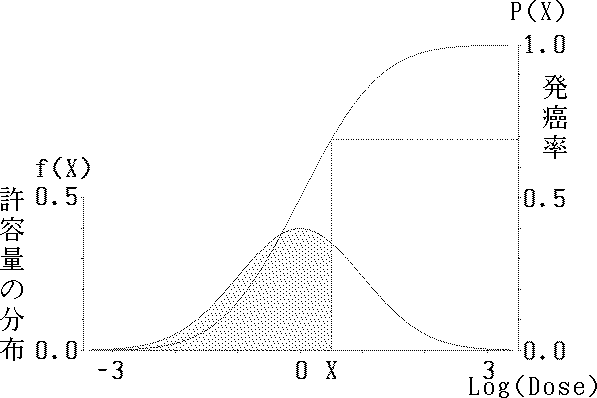
 図 1.プロビットモデルの概念図 |
「各個体の許容量の対数が,平均値 $\mu$ と標準偏差 $\sigma$ をパラメータとする正規分布に従う」とするモデルである( 図 1 参照 )。
\[ P = \Phi\left( \frac{\log D-\mu}{\sigma} \right) = \Phi\,(\alpha+\beta\ \log D) \tag{1} \] ( 1 )式で,$\Phi$ は標準正規分布関数 ( 累積度数分布関数 ) ,$P$ は発癌率,$D$ は用量である。
このモデルは,$D$ が $0$ に近付くと $P$ はほとんど $0$ になり,$D$ が大きくなるにつれて $1$ に近付く S 字形の用量 - 反応曲線を示す。 また,閾値の存在を仮定していないにもかかわらず,用量の減少に伴い,反応率は他のモデルに比べて,急速に $0$ に近付く。
 図 1.プロビットモデルの概念図 |