図 11 に示すように，投与された化学物質（ $C$ ）はそのまま排泄される部分（ $C_e$ ）と，活性化される部分（ $RM$ ）がある。$RM$ は無毒化される部分（ $IM$ ），遺伝子に関係しないタンパクなどと結合する部分（ $CBN$ ）のほか，DNA などと結合して $CBG$ となる。$CBG$ は，一部は修復されて $CBGR$ となるが，残りは $RCBG$ となり，プロモーション過程を経て癌が発生する。

図 11．Gehring のモデル

　このモデルでは，投与量 $D$ は $[C]$，有効用量は $[RCBG]$ となる（ $[　]$ は濃度を表す ）。$[RCBG]$ は $[CBG]$ と比例するので，$[CBG]$ を考えてもよい ）。これらの系は，（ 34 ），（ 35 ）式の 2 個の式で表現される。 \[ \begin{align*} &k_G\ [RM]-k_R\ [RCBG]-\displaystyle \frac{V_M^R\ [RCBG]}{k_M^R+[RCBG]}=0 \tag{34} \\[5pt] &(k_F+k_G)\ [RM]-\displaystyle \frac{V_M^D\ [RM]}{k_M^D+[RM]}-\frac{V_M^A\ [C]}{k_M^A+[C]}=0 \tag{35} \end{align*} \] 　$( V_M^A,\ k_M^A )$ ， $( k_M^D,\ k_M^D )$ ， $( V_M^R,\ k_M^R )$ はActivation，Detoxification，Repair の Michaelis - Menten パラメータ，$k_F$，$k_G$，$k_R$ は一次の速度常数。

　Michaelis - Menten パラメータをなんらかの方法で推定・測定すれば，有効用量を決定できる。有効用量が決定されたならば，今までに述べた用量 - 反応関数，例えばマルチステージモデルなどをあてはめればよい。

　このモデルでは，Michaelis - Menten パラメータが取る値によって投与量と有効用量の関係は図に示すように何通りかあるので，投与量の関数で表せないような広範囲の実験データを表現できる。特に，図 12 の c に示したような場合は，閾値の存在を示しているので興味深い（ (a) は first - order kinetics，(b) は activation system の飽和，(c) は detoxification または repair system の飽和，(d) は (b)，(c) の複合 ）。

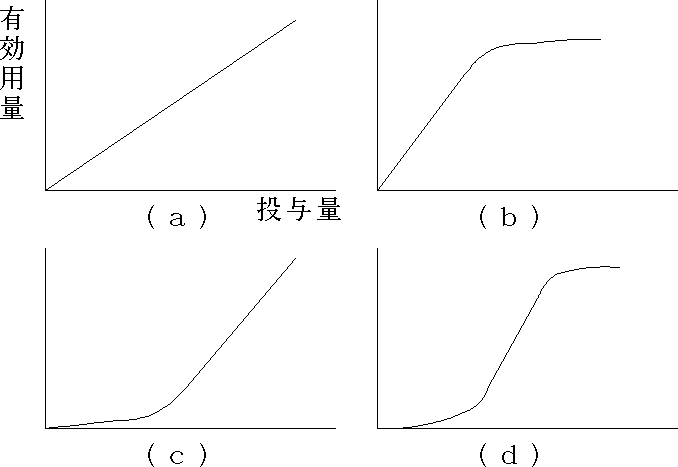図 12．投与量と有効用量の関係の模式図