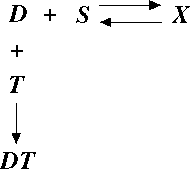図 10 に示すように，有害作用が発現する確率 $P ( D )$ は 投与された化学物質 $D$ が，活性化酵素 $S$ により活性化された化合物 $X$ に比例すると考える。

　もし，解毒酵素 $T$ による解毒作用が非可逆的ならばこの系の定常状態を考えれば（ 32 ）式のような閾値のある用量 - 反応関係が得られる。 ただし，$D \leqq T$ において反応が $0$ であるというのは，漸近的あるいは定常状態を考えた場合のことであり，実際には $D$ が解毒酵素 $T$ に結合する以前にも $X$ が生成されるので，厳密にいえば正確ではない。

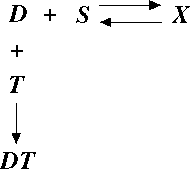図 10．Cornfield のモデル

\[ \left \{ \begin{array}{ll} P(D) = 0\ \ , & D \leqq T \\[5pt] P(D) = \displaystyle \frac{D-S\ P(D)-T}{D-S\ P(D)-T+K}\ \ , & D \gt T \end{array} \right . \tag{32} \]

\[ \left \{ \begin{align*} P(D)= &\ \displaystyle D\ S+K \left (1+\frac{T}{K^*} \right )\ \ , & D \leqq T\\[5pt] P(D)= &\ \displaystyle \frac{D-S\ P(D)-y}{D-S\ P(D)-y+K}\ \ , & D \gt T\\[5pt] & y = \displaystyle \frac{K\ P(D)\ T}{K\ P(D)+K^*\ \{1-P(D)\}} \end{align*} \right . \tag{33} \] 　いずれにせよ，Cornfield のモデルは化学物質の発癌作用に閾値が存在する可能性を示した点で意義が深い。