目的

抵抗直線（resistant line）を描く。

使用法

resistant.line(x, y, no.iteration=FALSE, n=1)

# print メソッド
print.resistant.line(obj, digits=5, sig=0.95)

# plot メソッド
plot.resistant.line(obj, posx="topleft", posy=NULL, xlab=obj$names.xy[1], ylab=obj$names.xy[2],	hist=FALSE, ...)

引数

x             独立変数
y             従属変数
no.iteration  繰り返し収束計算をしないときには TRUE を指定する
n             ブートストラップ法で信頼区間を求めるときの回数
              デフォルトは 1。この場合には信頼区間を求めない
obj           "resistant.line" オブジェクト
digits        表示桁数
sig           ブートストラップ法による信頼区間を求めるときの信頼度
posx, posy    legend 関数のための位置引数（"topleft", "bottomright" なども可）
xlab, ylab    軸の名前
hist          ブートストラップ法の結果のヒストグラムを描くかどうか
...           plot 関数に渡されるその他の引数

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/resistant_line.R", encoding="euc-jp")

# 抵抗直線を描く
resistant.line <- function(  x,                                      # 独立変数（横軸に取る）
                                y,                                      # 従属変数（縦軸に取る）
                                no.iteration=FALSE,                     # 収束計算をするかどうか
                                n=1)                                    # ブートストラップ法で信頼区間を求めるときの回数
{
        resistant.line0 <- function(x, y)
        {
                OK <- complete.cases(x, y)                           # 欠損値を持つケースを除く
                x <- x[OK]
                y <- y[OK]

                n <- length(x)                                               # データの組数
                o <- order(x)                                                # x の順序づけ
                x <- x[o]                                            # x を昇順に並べ替える
                y <- y[o]                                            # x，y を対応づけて並べ替える
                m <- floor(n/3)                                              # データを 3 分割するときの個数
                n1 <- 1:m                                            # 最初の 1/3 に対する添え字
                n2 <- (m+1): (n-m)                                   # 次の 1/3 に対する添え字
                n3 <- (n-m+1):n                                              # 最後の 1/3 に対する添え字
        
                m.x1 <- median(x[n1])                                        # 最初の 1/3 の中央値
                m.x2 <- median(x[n2])                                        # 次の 1/3 の中央値
                m.x3 <- median(x[n3])                                        # 最後の 1/3 の中央値
        
                a <- b <- 0                                               # 傾きと切片の初期値
                repeat {                                                # 収束計算
                        m.y1 <- median(y[n1])                                # 最初の 1/3 の中央値
                        m.y2 <- median(y[n2])                                # 次の 1/3 の中央値
                        m.y3 <- median(y[n3])                                # 最後の 1/3 の中央値
                        d.a <- (m.y3-m.y1)/(m.x3-m.x1)                       # 傾きの修正量
                        d.b <- (m.y1+m.y2+m.y3-d.a*(m.x1+m.x2+m.x3))/3       # 切片の修正量
                        a <- a+d.a                                   # 傾きの修正
                        b <- b+d.b                                   # 切片の修正
                        if (no.iteration || abs(d.a/a) < 1e-7) break # 収束計算をしない場合，収束した場合はループ脱出
                        y <- y-(d.a*x+d.b)                           # 抵抗直線で説明できる部分を取り除く
                }
                return(c(b, a))                                         # 結果を返す
        }
        Driver <- function(x, y)                                     # ブートストラップ法のためのドライバー
        {
                n <- length(x)
                suffix <- sample(n, n, replace=TRUE)                 # リサンプリング
                return(resistant.line0(x[suffix], y[suffix]))           # リサンプリングしたデータについてパラメータを推定
        }
        names.xy <- c(deparse(substitute(x)), deparse(substitute(y)))        # 変数名を控えておく
        ans <- list(coefficients=resistant.line0(x, y),                      # 引数に対してパラメータを推定する
                    names.xy=names.xy, x=x, y=y)
        if (n > 1) {
                ans2 <- replicate(n, Driver(x, y))                   # ブートストラップを n 回実行
                ans <- append(ans, list(intercepts=ans2[1,], slopes=ans2[2,]))
        }
        class(ans) <- "resistant.line"                                       # print, plot メソッドのためにクラス名をつけておく
        return(ans)
}
# print メソッド
print.resistant.line <- function(    obj,                            # "resistant.line" オブジェクト
                                        digits=5,                       # 表示桁数
                                        sig=0.95)                       # 信頼度
{
        if (length(obj) == 4) {
                cat("Intercept:", round(obj$coefficients[1], digits),
                    "    Slope:", round(obj$coefficients[2], digits), "\n")
        }
        else {
                alpha <- (1-sig)/2
                LCL <- c(quantile(obj$intercepts, alpha), quantile(obj$slopes, alpha))
                UCL <- c(quantile(obj$intercepts, 1-alpha), quantile(obj$slopes, 1-alpha))
                ans <- data.frame(obj$coefficients, LCL, UCL)
                dimnames(ans) <- list(c("Intercept:", "Slope:"),
                                      c("Estimate", paste(c(alpha, 1-alpha), "%", sep="")))
                print(ans, digits=digits)               
        }
}
# plot メソッド
plot.resistant.line <- function(obj,                                 # "resistant.line" オブジェクト
                        posx="topleft", posy=NULL,                      # legend 関数のための位置引数
                        xlab=obj$names.xy[1], ylab=obj$names.xy[2],     # 軸の名前
                        hist=FALSE,                                     # ヒストグラムを描くとき TRUE にする
                        ...)                                            # その他の任意の plot 関数の引数
{
        if (hist && length(obj) == 6) {                                   # ブートストラップの結果を，hist=TRUE のときに，ヒストグラムで表示する
                layout(matrix(1:2, 2))
                hist(obj$intercepts, xlab="Intercept", main="", right=FALSE)
                hist(obj$slopes, xlab="Slope", main="", right=FALSE)
                layout(1)
        }
        else {                                                          # 散布図と Deming 法の回帰直線と直線回帰式を表示する
                plot(obj$x, obj$y, xlab=xlab, ylab=ylab, ...)
                abline(obj$coefficients)
                abline(lm(obj$y~obj$x), lty=2, col=2)
                legend(posx, posy, legend=c("resistant line", "linear regression"), lty=1:2, col=1:2)
        }
}


使用例

x <- 1961:1993
y <- c(139.130, 140.293, 143.137, 147.350, 150.686, 144.317, 151.207,
152.882, 156.867, 155.749, 157.735, 162.962, 159.036, 158.589, 149.213,
148.725, 161.331, 161.363, 158.899, 142.862, 139.085, 162.026, 162.117,
163.621, 152.982, 170.722, 162.175, 144.809, 167.581, 185.984, 176.457,
134.477, 134.477)
resistant.line(x, y)
resistant.line(x, y, n=1000)

出力結果例

> resistant.line(x, y) # 点推定値と信頼区間を求める
Intercept: -1189.844     Slope: 0.68187 

> a <- resistant.line(x, y, n=1000) # 点推定値と信頼区間を求める

> print(a)

              Estimate      0.025%    0.975%
Intercept: -1189.84415 -1940.14227 1029.1491　信頼区間は毎回異なる
Slope:         0.68187    -0.44554    1.0624

> plot(a) # 散布図と抵抗直線および回帰直線



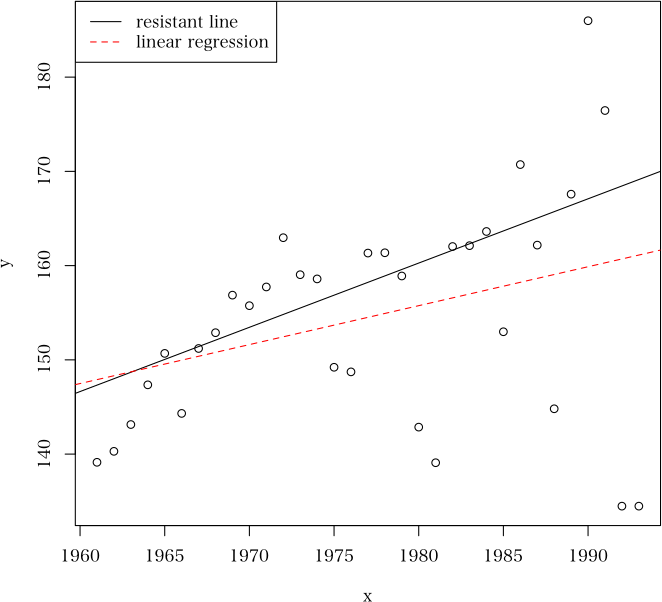> plot(a, hist=TRUE) # ブートストラップパラメータの分布図



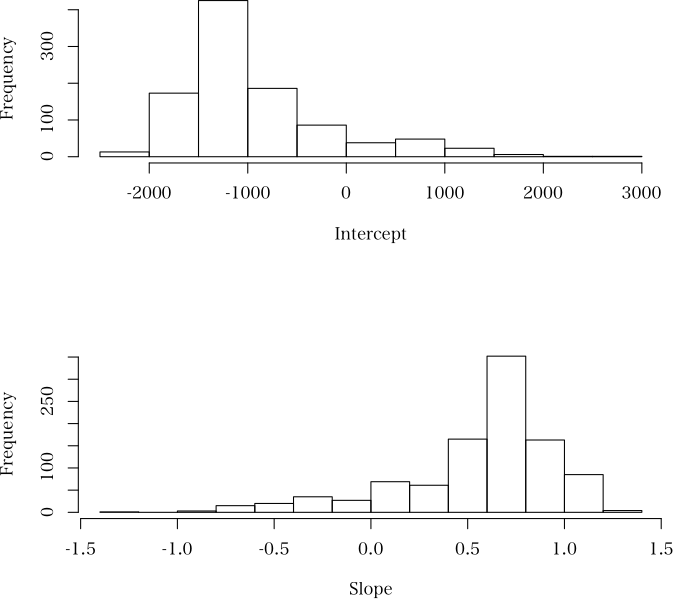> resistant.line(x, y) # 点推定値のみを求める

Intercept: -1189.844     Slope: 0.68187 

 解説ページ