数量化 I 類 Last modified: Sep 02, 2009
目的
数量化 I 類による分析を行う。
カテゴリー変数をダミー変数に変換すれば,R に元から備わっている
lm 関数で分析することにより本質的に同じ解を得ることができる。
しかも,lm を使えば,実際には自分でダミー変数に変換する必要すらない。
使用法
qt1(dat, group, func.name=c("solve", "ginv"))
print.qt1(obj, digits=5)
summary.qt1(obj, digits=5)
plot.qt1(obj, which=c("category.score", "fitness"), ...)
引数
dat データ行列またはデータ・フレーム
行がケース,列が変数。すべて factor であること
y 従属変数
func.name 逆行列を計算する関数名(solve か ginv)
正規方程式が特異行列になる場合以外はどちらを使っても結果は同じ
省略時は solve
ムーア・ペンローズ型一般化逆行列を使うときは ginv
obj qt1 が返すオブジェクト
digits 結果の表示桁数
which カテゴリースコアを描画するなら category.score,観察値と予測値を描画するなら fitness
ソース
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/qt1.R", encoding="euc-jp")
# 数量化 I 類
qt1 <- function(dat, # データ行列
y, # 従属変数
func.name=c("solve", "ginv")) # 逆行列を取る関数名の選択
{
vname <- colnames(dat) # 変数名
vname.y <- deparse(substitute(y))
cname <- unlist(sapply(dat, levels)) # カテゴリー名
dat <- data.frame(dat, y)
dat <- subset(dat, complete.cases(dat)) # 欠損値を持つケースを除く
p <- ncol(dat) # 最右端が従属変数,残りはカテゴリー変数
ncat <- p-1 # 最右端が従属変数,残りはカテゴリー変数
stopifnot(all(sapply(dat[, 1:ncat], is.factor))) # 独立変数はすべて factor であること
dat[, 1:ncat] <- lapply(dat[ ,1:ncat, drop=FALSE], as.integer)
nc <- nrow(dat) # 列数
mx <- sapply(dat[, 1:ncat, drop=FALSE], max) # 各カテゴリー変数の取る値の最大値
start <- c(0, cumsum(mx)[-ncat]) # 延べの順序番号
nobe <- sum(mx) # 延べカテゴリー数
# ダミー変数を使ったデータ行列に変換
x <- t(apply(dat, 1,
function(obs)
{
zeros <- numeric(nobe)
zeros[start+obs[1:ncat]] <- 1
c(zeros[-start-1], obs[ncat+1])
}
))
# 重回帰分析として解く
a <- cov(x)
ndim <- nobe-ncat
if (match.arg(func.name) == "solve") {
inverse <- solve
B <- inverse(a[1:ndim, 1:ndim], a[ndim+1, 1:ndim])
}
else {
library(MASS)
inverse <- ginv
B <- inverse(a[1:ndim, 1:ndim]) %*% a[ndim+1, 1:ndim]
}
m <- colMeans(x)
const <- m[ndim+1]-sum(B*m[1:ndim])
prediction <- x[,1:ndim]%*%as.matrix(B)+const
observed <- x[,ndim+1]
prediction <- cbind(observed, prediction, observed-prediction)
# 数量化 I 類としての解に変換
ncase <- nrow(dat)
s <- colSums(x)
name <- coef <- NULL
en <- 0
for (i in 1:ncat) {
st <- en+1
en <- st+mx[i]-2
target <- st:en
temp.mean <- sum(s[target]*B[target])/ncase
const <- const+temp.mean
coef <- c(coef, -temp.mean, B[target]-temp.mean)
}
coef <- c(coef, const)
names(coef) <- c(paste(rep(vname, mx), cname, sep="."), "定数項")
# アイテム変数と従属変数間の偏相関係数
par <- matrix(0, nrow=nc, ncol=ncat)
for (j in 1:nc) {
en <- 0
for (i in 1:ncat) {
st <- en+1
en <- st+mx[i]-2
target <- st:en
par[j, i] <- crossprod(x[j, target], B[target])
}
}
par <- cbind(par, observed)
r <- cor(par)
print(vname)
i <- inverse(r)
d <- diag(i)
partial.cor <- (-i/sqrt(outer(d, d)))[ncat+1, 1:ncat]
partial.t <- abs(partial.cor)*sqrt((nc-ncat-1)/(1-partial.cor^2))
partial.p <- pt(partial.t, nc-ncat-1, lower.tail=FALSE)*2
partial <- cbind(partial.cor, partial.t, partial.p)
coef <- as.matrix(coef)
colnames(coef) <- "カテゴリースコア"
colnames(prediction) <- c("観察値", "予測値", "残差")
colnames(partial) <- c("偏相関係数", "t 値", "P 値")
rownames(prediction) <- paste("#", 1:nc, sep="")
rownames(partial) <- vname
rownames(r) <- colnames(r) <- c(vname, vname.y)
return(structure(list(coefficients=as.matrix(coef),
r=r, partial=partial, prediction=prediction), class="qt1"))
}
# print メソッド
print.qt1 <- function( obj, # qt1 が返すオブジェクト
digits=5) # 結果の表示桁数
{
print(round(obj$coefficients, digits=digits))
}
# summary メソッド
summary.qt1 <- function(obj, # qt1 が返すオブジェクト
digits=5) # 結果の表示桁数
{
print.default(obj, digits=digits)
}
# plot メソッド
plot.qt1 <- function( obj, # qt1 が返すオブジェクト
which=c("category.score", "fitness"), # カテゴリースコアを表示するか観察値と予測値を表示するかの選択
...) # barplot, plot に引き渡す引数
{
if (match.arg(which) == "category.score") {
coefficients <- obj$coefficients[-length(obj$coefficients),]
coefficients <- rev(coefficients)
cname <- names(coefficients)
names(coefficients) <- NULL
barplot(coefficients, horiz=TRUE, xlab="カテゴリースコア", ...)
text(0, 1.2*(1:length(cname)-0.5), cname, pos=ifelse(coefficients > 0, 2, 4))
}
else {
result <- obj$prediction
plot(result[, 2], result[, 1], xlab="予測値", ylab="観察値", asp=1, ...)
abline(c(0,1))
}
}
使用例
> dat <- data.frame(x1=c(1,3,1,1,2,1,2,1,3,1), x2=c(2,2,2,1,3,3,2,1,2,1), x3=c(2,2,2,1,2,3,2,1,2,2))
> dat[, 1:3] <- lapply(dat, factor)
> y <- c(6837,7397,7195,6710,6670,6279,6601,4929,5471,6164)
> (a <- qt1(dat, y))
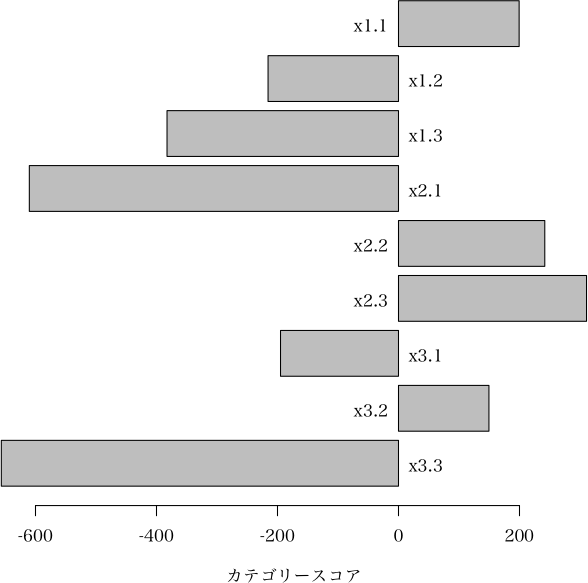
カテゴリースコア
x1.1 199.4
x1.2 -215.6
x1.3 -382.6
x2.1 -610.2
x2.2 241.8
x2.3 310.8
x3.1 -195.0
x3.2 149.5
x3.3 -656.5
定数項 6425.3
> summary(a)
$coefficients
カテゴリースコア
x1.1 199.4
x1.2 -215.6
x1.3 -382.6
x2.1 -610.2
x2.2 241.8
x2.3 310.8
x3.1 -195.0
x3.2 149.5
x3.3 -656.5
定数項 6425.3
$r # 相関係数
x1 x2 x3 y
x1 1.00000 -0.51066 -0.46318 -0.10328
x2 -0.51066 1.00000 0.16479 0.44059
x3 -0.46318 0.16479 1.00000 0.29052
y -0.10328 0.44059 0.29052 1.00000
$partial
偏相関係数 t 値 P 値
x1 0.30875 0.79512 0.45684
x2 0.50094 1.41777 0.20604
x3 0.35840 0.94035 0.38333
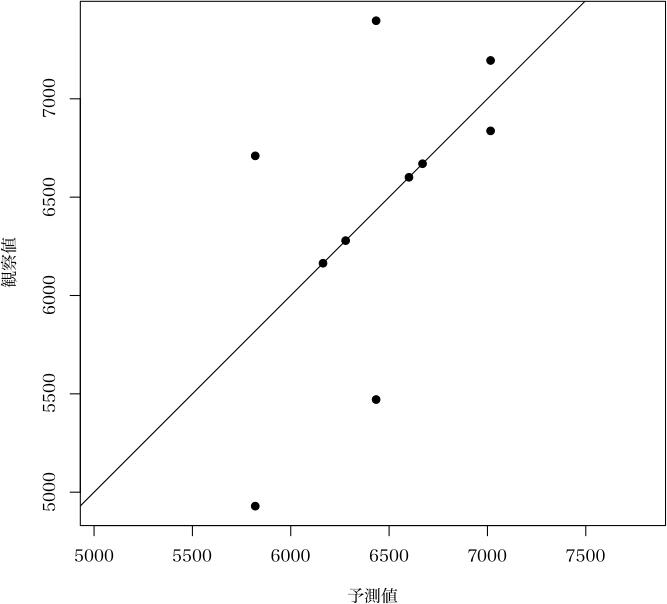
$prediction
観察値 予測値 残差
#1 6837 7016.0 -179.0
#2 7397 6434.0 963.0
#3 7195 7016.0 179.0
#4 6710 5819.5 890.5
#5 6670 6670.0 0.0
#6 6279 6279.0 0.0
#7 6601 6601.0 0.0
#8 4929 5819.5 -890.5
#9 5471 6434.0 -963.0
#10 6164 6164.0 0.0
attr(,"class")
[1] "qt1"
> plot(a)
 > plot(a, which="fitness", pch=19)
> plot(a, which="fitness", pch=19)
lm を使って分析する手順
> dat2 <- data.frame(dat, y)
> result <- lm(y ~ x1+x2+x3, data=dat2)
> summary(result)
Call:
lm(formula = y ~ x1 + x2 + x3, data = dat2)
Residuals:
1 2 3 4 5 6 7 8 9
-1.790e+02 9.630e+02 1.790e+02 8.905e+02 -7.105e-14 -8.527e-14 1.563e-13 -8.905e+02 -9.630e+02
10
-8.527e-14
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5819.5 764.3 7.614 0.0047 **
x12 -415.0 1323.8 -0.313 0.7744
x13 -582.0 1080.9 -0.538 0.6276
x22 852.0 1323.8 0.644 0.5656
x23 921.0 2022.1 0.455 0.6797
x32 344.5 1323.8 0.260 0.8115
x33 -461.5 2416.9 -0.191 0.8608
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1081 on 3 degrees of freedom
Multiple R-squared: 0.3151, Adjusted R-squared: -1.055
F-statistic: 0.23 on 6 and 3 DF, p-value: 0.9402
予測値は以下のようになっている(qt1 による予測値と同じ)
1 2 3 4 5 6 7 8 9 10
7016.0 6434.0 7016.0 5819.5 6670.0 6279.0 6601.0 5819.5 6434.0 6164.0
数量化 I 類の表現に導くには,以下のようにする。
元のデータの第 1 列の反応例数は
> xtabs(~dat$x1)
dat$x1
1 2 3
6 2 2
x1=2, x=3 の例数とそれに対応する係数の積和を求め全例数(6+2+2)で割ると平均スコアになる。
> sum(xtabs(~dat$x1)[2:3]*result$coefficients[2:3])/length(dat$x1)
[1] -199.4
これは,x1=1 のときを 0 としたときの平均スコアなので,平均スコアが 0 になるようにするには,
-199.4 だけスコアを小さくしてやればよい(今の場合は,199.4 大きくするということ)。
すなわち,x1=1,x1=2,x1=3 に対応するカテゴリースコアは
(0, -415, -582) のそれぞれから -199.4 を引けばよい。
最初の数値が,fd11 に対応するカテゴリースコア。
> c(0, result$coefficients[2:3])-(-199.4)
x12 x13
199.4 -215.6 -382.6
これを全てのアイテム変数について行い,最後に定数項の調整をする。
x1,x2,x3 について,カテゴリースコアを計算するために調整した数値の和は,
199.4-610.2-195.0 = -605.8
これを定数項で調整するため,
5819.5-(-605.8) = 6425.3
名義尺度変数を単純に 0/1 変数に変換しただけでは,冗長性があるので,
普通は問題が生じるが,R では一応ちゃんと答えを出すことができる。
以下の make.dummy 関数などにより,0/1 データに直す
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/make.dummy.R", encoding="euc-jp")
# アイテムデータをカテゴリーデータに変換する
make.dummy <- function(dat)
{
ncat <- ncol(dat)
dat[, 1:ncat] <- lapply(dat, function(x) {
if (is.factor(x)) {
return(as.integer(x))
}
else {
return(x)
}
})
mx <- sapply(dat, max)
start <- c(0, cumsum(mx)[1:(ncat-1)])
nobe <- sum(mx)
t(apply(dat, 1, function(obs) 1:nobe %in% (start+obs))) + 0
}
> d <- make.dummy(dat[,1:3])
> d
Cat-1-1 Cat-1-2 Cat-1-3 Cat-2-1 Cat-2-2 Cat-2-3 Cat-3-1 Cat-3-2 Cat-3-3
[1,] 1 0 0 0 1 0 0 1 0
[2,] 0 0 1 0 1 0 0 1 0
[3,] 1 0 0 0 1 0 0 1 0
[4,] 1 0 0 1 0 0 1 0 0
[5,] 0 1 0 0 0 1 0 1 0
[6,] 1 0 0 0 0 1 0 0 1
[7,] 0 1 0 0 1 0 0 1 0
[8,] 1 0 0 1 0 0 1 0 0
[9,] 0 0 1 0 1 0 0 1 0
[10,] 1 0 0 1 0 0 0 1 0
> summary(lm(y ~ d))
Call:
lm(formula = y ~ d)
Residuals:
1 2 3 4 5 6 7 8 9 10
-1.790e+02 9.630e+02 1.790e+02 8.905e+02 2.668e-13 -4.296e-13 -3.017e-13 -8.905e+02 -9.630e+02 -3.443e-13
Coefficients: (3 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5697.0 1528.6 3.727 0.0336 *
dCat-1-1 582.0 1080.9 0.538 0.6276
dCat-1-2 167.0 1323.8 0.126 0.9076
dCat-1-3 NA NA NA NA
dCat-2-1 -921.0 2022.1 -0.455 0.6797
dCat-2-2 -69.0 1528.6 -0.045 0.9668
dCat-2-3 NA NA NA NA
dCat-3-1 461.5 2416.9 0.191 0.8608
dCat-3-2 806.0 2022.1 0.399 0.7169
dCat-3-3 NA NA NA NA
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1081 on 3 degrees of freedom
Multiple R-Squared: 0.3151, Adjusted R-squared: -1.055
F-statistic: 0.23 on 6 and 3 DF, p-value: 0.9402
 解説ページ
解説ページ
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI

 > plot(a, which="fitness", pch=19)
> plot(a, which="fitness", pch=19)
