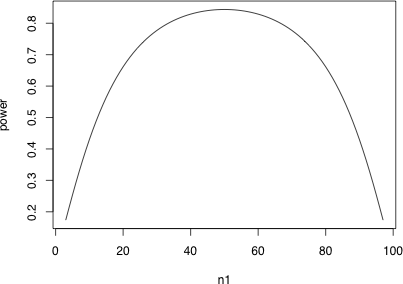
50 ずつにしたときが最も検出力が高い。
目的
二群の平均値の差の検定(両側検定)において,二群のサンプルサイズが異なるときの検出力を求める。
R には,power.t.test という関数があり,
二群のサンプルサイズが同じであるときのパワーアナリシスを行うことができる。
使用法
power.t.test2(n1, n2, delta, sig.level=0.05)
引数
n1, n2 両群のサンプルサイズ
delta 効果量
sig.level 有意水準(省略時には 0.05 が仮定される)
ソース
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/power_t_test2.R", encoding="euc-jp")
# 二群の平均値の差(両側検定)において,二群のサンプルサイズが異なるときの検出力を求める
power.t.test2 <- function( n1, # サンプルサイズ
n2, # サンプルサイズ
delta, # 効果量
sig.level=0.05) # 有意水準
{
phi <- n1+n2-2 # 自由度
lambda <- sqrt(n1*n2/(n1+n2))*delta
q <- qt(sig.level/2, phi, lower.tail=FALSE)
return(pt(-q, phi, ncp=lambda)+pt(q, phi, ncp=lambda, lower.tail=FALSE))
}
使用例
> power.t.test2(10, 8, 0.6)
[1] 0.2214264
全体で 100 のサンプルを採るとき,
サンプルサイズをどのように配分したら最も検出力が高くなるか。
> n <- 100
> n1 <- 3:(n-3)
> power <- sapply(n1, function(n1) { n2 <- n-n1; power.t.test2(n1, n2, 0.6) })
> pdf("power.pdf", width=6, height=5)
> plot(n1, power,type="l")
> dev.off()

50 ずつにしたときが最も検出力が高い。