図形描画関数群 Last modified: May 18, 2009
目的
図形描画のための関数群を提供する。
使用法・引数
- plot.start(x1=0, y1=0, x2=500, y2=500, ...)
プロット関数群の開始。
(x1, y1)-(x2, y2) 描画領域の左下隅と右上隅の座標を宣言する。
普通に R の関数(hist や plot などなど)を使って描かれたグラフに以下の関数を使って図形を付加する場合には不要。
縦横比を1にするためには,asp=1 を加えること。
- plot.line(x1, y1, x2, y2, ...)
(x1, y1)-(x2, y2) を結ぶ直線を描画する。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
- plot.hline(x1, x2, y, ...)
(x1, y)-(x2, y) を結ぶ水平な直線を描画する。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
- plot.vline(x, y1, y2, ...)
(x, y1)-(x, y2) を結ぶ垂直な直線を描画する。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
- plot.box(x1, y1, x2, y2, ...)
(x1, y1)-(x2, y2) を対角頂点とする長方形(正方形)を描画する。
実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
- plot.circle(ox, oy, r, start=0, end=360, ...)
中心を (ox, oy) とする,半径 r の円を描く。
start, end には,描き始めと描き終わりの位置を指定できる。水平線を基準として,角度(度単位)で指定できる(0, 360 とすると,完全な円を描くことになる。90, 270 とすると,左半分の円を描くことを指示することになる)。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
- plot.circlef(ox, oy, r, ...)
中心を (ox, oy) とする,半径 r の円を描き,内部を塗りつぶす。
実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
- plot.ellipse(ox, oy, ra, rb, phi=0, start=0, end=360, ...)
中心を (ox, oy) とする,長径 ra,短径 rb の楕円を描く。
phi は楕円の傾き(長径が水平線となす角度),start, end には,描き始めと描き終わりの位置を指定できる。長径を基準として,角度(度単位)で指定できる(0, 360 とすると,完全な楕円を描くことになる。90, 270 とすると,左半分の楕円を描くことを指示することになる)。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
- plot.ellipsef(ox, oy, ra, rb, phi=0, ...)
中心を (ox, oy) とする,長径 ra,短径 rb の楕円を描き,内部を塗りつぶす。
phi は楕円の傾き(長径が水平線となす角度)。
実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
- plot.polygon(x1, y1, l, n, ...)
(x1, y1) を描きはじめとして,右方向へ水平
に l の長さの辺を描きその後反時計回りに辺を構成して n 正方角形を描く
。
実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
- plot.polygon2(ox, oy, r, n, phi=90, ...)
(ox, oy) 中心とする円に内接する正 n 角形を描画する。
最初の頂点の位置は phi 引数(度)によって,反時計回りに再設定できる。
実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
- plot.grid(x1, y1, x2, y2, wx, wy=NULL, ...)
(x1, y1)-(x2, y2) を対角頂点とする長方形(正方形)を描画し,横方向の間隔が wx, 縦方向の間隔が wy となる格子を描く。
実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
長方形内部を塗りつぶすには,前もって plot.box で塗りつぶした長方形を描いてから plot.grid 関数を使う。
- radian(degree)
度をラジアンに変換する
ソース
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/plot.R", encoding="euc-jp")
# 図形描画のための関数群
# プロット関数群の開始。
# (x1, y1)-(x2, y2) 描画領域の左下隅と右上隅の座標を宣言する。
# 普通に R の関数(hist や plot などなど)を使って描かれたグラフに以下の関数を使って図形を付加する場合には不要。
plot.start <- function(x1=0, y1=0, x2=500, y2=500, ...)
{
plot(c(x1, x2), c(y1, y2), type="n", xlab="", xaxt="n", ylab="", yaxt="n", bty="n", ...)
}
# (x1, y1)-(x2, y2) を結ぶ直線を描画する。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
plot.line <- function(x1, y1, x2, y2, ...)
{
lines(c(x1, x2), c(y1, y2), ...)
}
# (x1, y)-(x2, y) を結ぶ水平な直線を描画する。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
plot.hline <- function(x1, x2, y, ...)
{
lines(c(x1, x2), c(y, y), ...)
}
# (x, y1)-(x, y2) を結ぶ垂直な直線を描画する。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
plot.vline <- function(x, y1, y2, ...)
{
lines(c(x, x), c(y1, y2), ...)
}
# (x1, y1)-(x2, y2) を対角頂点とする長方形(正方形)を描画する。
# 実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
plot.box <- function(x1, y1, x2, y2, ...)
{
polygon(c(x1, x2, x2, x1), c(y1, y1, y2, y2), ...)
}
# 中心を (ox, oy) とする,半径 r の円を描く。
# start, end には,描き始めと描き終わりの位置を指定できる。
# 水平線を基準として,角度(度単位)で指定できる(0, 360 とすると,完全な円を描くことになる。
# 90, 270 とすると,左半分の円を描くことを指示することになる)。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
plot.circle <- function(ox, oy, r, start=0, end=360, ...)
{
plot.ellipse(ox, oy, r, r, 0, start, end, ...)
}
# 中心を (ox, oy) とする,半径 r の円を描き,内部を塗りつぶす。
# 実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
plot.circlef <- function(ox, oy, r, ...)
{
plot.ellipse(ox, oy, r, r, 0, 0, 360, func=polygon, ...)
}
# 度をラジアンに変換する
radian <- function(degree) {
degree/180*pi
}
# 中心を (ox, oy) とする,長径 ra,短径 rb の楕円を描く。
# phi は楕円の傾き(長径が水平線となす角度),start, end には,描き始めと描き終わりの位置を指定できる。
# 長径を基準として,角度(度単位)で指定できる(0, 360 とすると,完全な楕円を描くことになる。
# 90, 270 とすると,左半分の楕円を描くことを指示することになる)。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
plot.ellipse <- function(ox, oy, ra, rb, phi=0, start=0, end=360, length=100, func=lines, ...)
{
theta <- c(seq(radian(start), radian(end), length=length), radian(end))
if (phi == 0) {
func(ra*cos(theta)+ox, rb*sin(theta)+oy, ...)
}
else {
x <- ra*cos(theta)
y <- rb*sin(theta)
phi <- radian(phi)
cosine <- cos(phi)
sine <- sin(phi)
func(cosine*x-sine*y+ox, sine*x+cosine*y+oy, ...)
}
}
# 中心を (ox, oy) とする,長径 ra,短径 rb の楕円を描き,内部を塗りつぶす。
# phi は楕円の傾き(長径が水平線となす角度)。
# 実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
plot.ellipsef <- function(ox, oy, ra, rb, phi=0, ...)
{
plot.ellipse(ox, oy, ra, rb, phi, 0, 360, func=polygon, ...)
}
# (x1, y1) を描きはじめとして,右方向へ水平に l の長さの辺を描きその後反時計回りに辺を構成して n 正方角形を描く。
# 実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
plot.polygon <- function(x1, y1, l, n, ...)
{
theta <- seq(0, 2*pi, length=n+1)
x <- rep(x1, n)
y <- rep(y1, n)
for (i in 2:n) {
x[i] <- x[i-1]+l*cos(theta[i])
y[i] <- y[i-1]+l*sin(theta[i])
}
polygon(x, y, ...)
}
# (ox, oy) 中心とする円に内接する正 n 角形を描画する。
# 最初の頂点の位置は phi 引数(度)によって,反時計回りに再設定できる。
# 実際には polygon 関数を呼ぶので,... には polygon 関数が許容する引数を書くことができる。
plot.polygon2 <- function(ox, oy, r, n, phi=90, ...)
{
theta <- seq(0, 2*pi, length=n+1)+radian(phi)
polygon(r*cos(theta)+ox, r*sin(theta)+oy, ...)
}
# (x1, y1)-(x2, y2) を対角頂点とする長方形(正方形)を描画し,横方向の間隔が wx, 縦方向の間隔が wy となる格子を描く。
# 実際には lines 関数を呼ぶので,... には lines 関数が許容する引数を書くことができる。
# 長方形内部を塗りつぶすには,前もって plot.box で塗りつぶした長方形を描いてから plot.grid 関数を使う。
plot.grid <- function(x1, y1, x2, y2, wx, wy=NULL, ...)
{
X1 <- min(x1, x2)
X2 <- max(x1, x2)
Y1 <- min(y1, y2)
Y2 <- max(y1, y2)
for (i in 0:as.integer(abs(X2-X1)/wx)) {
plot.line(X1+wx*i, Y1, X1+wx*i, Y2, ...)
}
if (is.null(wy)) wy <- wx
for (i in 0:as.integer(abs(y2-y1)/wy)) {
plot.line(X1, Y1+wy*i, X2, Y1+wy*i, ...)
}
}
使用例
plot.start(asp=1)
t <- seq(0, 360, by=3)
l <- 130
ox <- l*cos(radian(t))
oy <- l*sin(radian(t))
for (i in 1:length(t)) plot.circle(ox[i]+250, oy[i]+250, abs(ox[i]), 0, 360, col="blue")
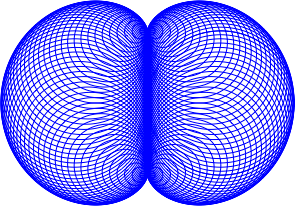 ネフロイド(包絡線が,腎臓に似ていると言うことで)
plot.start(asp=1)
t <- seq(0, 360, by=5)
l <- 100
ox <- l*cos(radian(t))
oy <- l*sin(radian(t))
for (i in 1:length(t)) plot.circle(ox[i]+320, oy[i]+250, sqrt((ox[i]-ox[1])^2+(oy[i]-oy[1])^2), 0, 360, col="blue")
ネフロイド(包絡線が,腎臓に似ていると言うことで)
plot.start(asp=1)
t <- seq(0, 360, by=5)
l <- 100
ox <- l*cos(radian(t))
oy <- l*sin(radian(t))
for (i in 1:length(t)) plot.circle(ox[i]+320, oy[i]+250, sqrt((ox[i]-ox[1])^2+(oy[i]-oy[1])^2), 0, 360, col="blue")
 カージオイド(包絡線が,心臓に似ていると言うことで)
plot.start(asp=1)
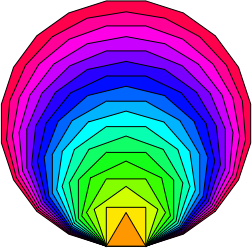
for (i in 20:3) plot.polygon(270, 10, 70, i, col=rainbow(20)[i])
カージオイド(包絡線が,心臓に似ていると言うことで)
plot.start(asp=1)
for (i in 20:3) plot.polygon(270, 10, 70, i, col=rainbow(20)[i])
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI

 ネフロイド(包絡線が,腎臓に似ていると言うことで)
plot.start(asp=1)
t <- seq(0, 360, by=5)
l <- 100
ox <- l*cos(radian(t))
oy <- l*sin(radian(t))
for (i in 1:length(t)) plot.circle(ox[i]+320, oy[i]+250, sqrt((ox[i]-ox[1])^2+(oy[i]-oy[1])^2), 0, 360, col="blue")
ネフロイド(包絡線が,腎臓に似ていると言うことで)
plot.start(asp=1)
t <- seq(0, 360, by=5)
l <- 100
ox <- l*cos(radian(t))
oy <- l*sin(radian(t))
for (i in 1:length(t)) plot.circle(ox[i]+320, oy[i]+250, sqrt((ox[i]-ox[1])^2+(oy[i]-oy[1])^2), 0, 360, col="blue")
 カージオイド(包絡線が,心臓に似ていると言うことで)
plot.start(asp=1)
for (i in 20:3) plot.polygon(270, 10, 70, i, col=rainbow(20)[i])
カージオイド(包絡線が,心臓に似ていると言うことで)
plot.start(asp=1)
for (i in 20:3) plot.polygon(270, 10, 70, i, col=rainbow(20)[i])
