因子分析 Last modified: Aug 31, 2009
目的
因子分析を行う。
R には factanal という関数が用意されている。最尤法により因子を求めプロマックス回転するならそれを利用すべきである。
factanal を使いやすくする関数（factanal2）を作ったので参照されたい。
使用法
pfa(dat)
pfa(dat, method=c("Varimax", "biQuartimax", "Quartimax", "Equimax", "None"), eps1=1e-5, eps2=1e-5, max1=999, max2=999, factors=0)
print(result, before=FALSE)
plot(result, before=FALSE, fac.no=1:2, scores=FALSE, xlab=NULL, ylab=NULL, axis=TRUE, label.cex=0.7, ...)
引数
dat データ行列（行がケース，列が変数）。欠損値 NA を含むケース（行）は分析に先だって自動的に削除される。
または，相関係数行列（正方行列であること）
method 因子軸の回転方法の指定（使用法参照 回転しないときは None）
eps1 共通性の反復推定の終了判定条件
eps2 因子軸の回転の終了判定条件
max1 共通性の反復推定の回数の上限
max2 因子軸の回転の回数の上限
factors 求める因子の数（指定しない場合には，固有値が 1 以上の数になる）
result pfa が返すオブジェクト
before 因子軸の回転前の結果を使うか回転後の結果を使うかを指定
fac.no 横軸と縦軸にプロットする因子番号
scores 因子得点を描くか因子負荷量を描くかの指定
xlab 横軸の名前
ylab 縦軸の名前
axis 座標軸を描くかどうかの指定
label.cex 描画点につけるラベルの文字の大きさ
... plot 関数に引き渡す引数
ソース
インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/pfa.R", encoding="euc-jp")
# 因子分析
pfa <- function(dat, # データ行列または相関係数行列
method=c("Varimax", "biQuartimax", "Quartimax", "Equimax", "None"), # 回転法
eps1=1e-5, # 共通性の収束限界
eps2=1e-5, # バリマックス回転の収束限界
max1=999, # 共通性の推定のための収束計算の上限回数
max2=999, # バリマックス回転を行う上限回数
factors=0)
{
method <- match.arg(method) # 回転法を補完
dat <- subset(dat, complete.cases(dat)) # 欠損値を持つケースを除く
nr <- nrow(dat) # ケース数
nc <- ncol(dat) # 変数の個数
if (is.null(colnames(dat))) { # 変数名が無いときには仮の名前を付ける
colnames(dat) <- paste("Var", 1:nc, sep=".")
}
vnames <- colnames(dat) # 変数名を記録
if (nr != nc && is.null(rownames(dat))) { # ケース名がないときには仮の名前を付ける
rownames(dat) <- paste("Obs", 1:nr, sep=".")
}
cnames <- rownames(dat) # ケース名を記録
r0 <- r <- if (nr == nc) dat else cor(dat) # 与えられたのがデータ行列なら，相関係数行列を計算する
communality0 <- 1-1/diag(solve(r)) # 共通性の初期値（SMC）
diag(r) <- communality0 # 相関係数行列の対角成分を共通性で置き換える
result <- eigen(r) # 固有値・固有ベクトルを求める
eval <- result$values # 固有値
evec <- result$vectors # 固有ベクトル
if (factors == 0) { # 因子数の指定がないときには，
factors <- sum(eval >= 1) # 1 以上の固有値の数とする
}
converged <- FALSE # 共通性の収束計算を行う
for (i in 1:max1) { # 上限回数まで繰り返す
eval <- eval[1:factors] # 必要な因子数まで，固有値を取る
evec <- evec[,1:factors] # 必要な因子数まで
evec <- t(sqrt(eval)*t(evec)) # 因子負荷量を計算
r <- r0 # 相関係数行列を復帰
communality <- rowSums(evec^2) # 共通性を計算
if (all(abs(communality-communality0) < eps1)) { # 共通性の変化が限界以内になれば，
converged <- TRUE # 収束したとして，
break # ループを抜ける
}
communality0 <- communality # 現在の共通性を保存
diag(r) <- communality # 相関係数行列の対角成分を置き換える
result <- eigen(r) # 固有値・固有ベクトルを求める
eval <- result$values # 固有値
evec <- result$vectors # 固有ベクトル
}
if (converged == FALSE) { # 収束フラッグが FALSE なら，
warning("Not converged.") # 収束しなかったと警告する
}
else if (any(communality >= 1)) { # 1 を超える共通性があったら，
warning("Communality >= 1.") # 警告する
}
if (factors == 1 || method == "None") { # 因子数が 1 であるか，因子軸の回転をしないのなら，
w <- solve(r0)%*%evec # 因子得点係数を計算する
scores <- (scale(dat)*sqrt(nr/(nr-1)))%*%w # 因子得点を計算する
rownames(evec) <- names(communality) <- vnames # 名前を付けて，結果を返す
rownames(scores) <- cnames
colnames(scores) <- colnames(evec) <- names(eval) <- paste("FAC", 1:factors, sep=".")
return(structure(list(rotation=method, correlation.matrix=r0, communality=communality,
before.rotation.fl=evec, before.rotation.eval=eval, scores=scores), class="pfa"))
}
else { # 因子軸を回転するなら，
fl <- evec/sqrt(communality) # 因子負荷量を共通性で基準化
eig <- numeric(factors)
ov <- 0
wt <- switch (method, # 回転方法によって，重みを変える
"Varimax" = 1,
"biQuartimax" = 0.5,
"Quartimax" = 0,
"Equimax" = nc/2)
fnp <- nc
for (loop in 1:max2) { # 回転の上限回数まで収束計算
for (k in 1:(factors-1)) {
for (k1 in (k+1):factors) {
x <- fl[,k]
y <- fl[,k1]
xy <- x^2-y^2
a <- sum(xy)
b <- 2*sum(x*y)
c <- sum(xy^2-4*x^2*y^2)
d <- 4*sum(x*y*xy)
dd <- d-2*wt*a*b/fnp
theta <- atan(dd/(c-wt*(a^2-b^2)/fnp))
if(sin(theta)*dd < 0) {
if (theta > 0) {
theta <- theta-pi
}
else {
theta <- theta+pi
}
}
theta <- theta/4
cs <- cos(theta)
si <- sin(theta)
fljk <- fl[,k]
fljk1 <- fl[,k1]
fl[,k] <- fljk*cs+fljk1*si
fl[,k1] <- fljk1*cs-fljk*si
}
}
v <- sum((t(fl)^2-colSums(fl^2)*wt/fnp)^2)
if (abs(v-ov) < eps2) { # 収束したら，
break # ループから抜ける
}
ov <- v
}
fl <- fl*sqrt(communality) # 因子負荷量
w <- solve(r0)%*%fl # 因子得点係数
scores <- (scale(dat)*sqrt(nr/(nr-1)))%*%w # 因子得点
eval2 <- colSums(fl^2) # 因子負荷量の二乗和
rownames(evec) <- rownames(fl) <- names(communality) <- vnames
rownames(scores) <- cnames
colnames(scores) <- colnames(evec) <- colnames(fl) <- names(eval) <- names(eval2) <- paste("FAC", 1:factors, sep=".")
return(structure(list(rotation=method, correlation.matrix=r0, communality=communality,
before.rotation.fl=evec, before.rotation.eval=eval,
after.rotation.fl=fl, after.rotation.eval=eval2, scores=scores), class="pfa"))
}
}
# print メソッド
print.pfa <- function( result, # pfa が返すオブジェクト
before=FALSE)
{
communality <- result$communality
vnames <- sapply(names(communality), function(i) substring(i, 1, min(nchar(i), 7)))
if (before || is.null(result$after.rotation.fl)) {
fl <- result$before.rotation.fl
eval <- result$before.rotation.eval
label <- "E-value"
if (result$rotation == "None") {
printf("\nResult without rotation\n\n")
}
else {
printf("\nBefore %s rotation\n\n", result$rotation)
}
}
else {
fl <- result$after.rotation.fl
eval <- result$after.rotation.eval
label <- "Sq.Sum"
printf("\nAfter %s rotation\n\n", result$rotation)
}
nv <- nrow(fl)
nc <- ncol(fl)
cat(" ", sprintf(" Fac.%02i", 1:nc), " Communality\n", sep="")
for (i in 1:nv) {
cat(sprintf("%-7s", vnames[i]), sprintf("%7.3f", fl[i,]), sprintf("%7.3f\n", communality[i]), sep="")
}
cat(sprintf("%-7s", label), sprintf("%7.3f", eval), "\n", sep="")
cat(sprintf("%-7s", "Cont."), sprintf("%7.1f", eval/nv*100), "\n", sep="")
cat(sprintf("%-7s", "Cum."), sprintf("%7.1f", cumsum(eval/nv*100)), "\n", sep="")
}
# plot メソッド
plot.pfa <- function( result, # pfa が返すオブジェクト
before=FALSE, # 因子軸の回転前の結果を使うか回転後の結果を使うかを指定
fac.no=1:2, # 横軸と縦軸にプロットする因子番号
scores=FALSE, # 因子得点を描くか因子負荷量を描くかの指定
xlab=NULL, ylab=NULL, # 横軸，縦軸の名前
axis=TRUE, # 座標軸を描くかどうかの指定
label.cex=0.7, # 描画点につけるラベルの文字の大きさ
...) # plot 関数に引き渡す引数
{
fac.name <- names(result$before.rotation.eval)
if (length(fac.name) > 1) {
ax1 <- fac.no[1]
ax2 <- fac.no[2]
if (is.null(xlab)) {
xlab <- fac.name[ax1]
}
if (is.null(ylab)) {
ylab <- fac.name[ax2]
}
if (scores) {
x <- result$scores[, ax1]
y <- result$scores[, ax2]
labels <- 1:length(x)
}
else {
if (before || is.na(result$after.rotation.fl)) {
fl <- result$before.rotation.fl
}
else {
fl <- result$after.rotation.fl
}
x <- fl[, ax1]
y <- fl[, ax2]
labels <- names(result$communality)
}
plot(x, y, xlab=xlab, ylab=ylab, ...)
old <- par(xpd=TRUE)
text(x, y, labels, cex=label.cex, pos=1)
par(old)
}
if (axis) {
abline(h=0, v=0)
}
}
使用例 1
> dat <- read.table("pfa.data", header=TRUE) # ファイルからデータを読んだ
> dat
var1 var2 var3 var4 var5 var6 var7 var8 var9 var10
1 935 955 926 585 1010 925 1028 807 769 767
2 817 905 901 632 1004 950 957 844 781 738
3 768 825 859 662 893 900 981 759 868 732
4 869 915 856 448 867 874 884 802 804 857
5 787 878 880 592 871 874 884 781 782 807
6 738 848 850 569 814 950 957 700 870 764
7 763 862 839 658 887 900 1005 604 709 753
8 795 890 841 670 853 874 859 701 680 772
9 903 877 919 460 818 849 884 700 718 716
10 761 765 881 485 846 900 981 728 781 714
11 747 792 800 564 796 849 932 682 746 767
12 771 802 840 609 824 874 859 668 704 710
13 785 878 805 527 911 680 884 728 709 747
14 657 773 820 612 810 849 909 698 746 771
15 696 785 791 578 774 725 932 765 706 795
16 724 785 870 509 746 849 807 763 724 760
17 712 829 838 516 875 725 807 754 762 585
18 756 863 815 474 873 725 957 624 655 620
19 622 759 786 619 820 769 807 673 698 695
20 668 753 751 551 834 849 807 601 655 642
> ( result <- pfa(dat, factors=3) ) # 因子分析を実行
After Varimax rotation
Fac.01 Fac.02 Fac.03 Communality
var1 -0.818 0.381 -0.254 0.878
var2 -0.867 0.226 -0.054 0.806
var3 -0.581 0.619 -0.133 0.738
var4 0.041 0.070 0.730 0.539
var5 -0.834 0.026 0.315 0.796
var6 -0.187 0.631 0.371 0.571
var7 -0.412 0.339 0.317 0.385
var8 -0.349 0.560 -0.149 0.457
var9 -0.118 0.734 0.125 0.568
var10 -0.086 0.562 0.055 0.326
Sq.Sum 2.803 2.265 0.997
Cont. 28.0 22.7 10.0
Cum. 28.0 50.7 60.7
その他の結果は，str(result) のようにして要素を確認後，
個別の要素を print 関数によって出力する
> print(result$correlation, digits=3) # 相関係数行列
var1 var2 var3 var4 var5 var6 var7 var8 var9 var10
var1 1.000 0.8449 0.775 -0.2257 0.5586 0.375 0.429 0.4447 0.2466 0.3362
var2 0.845 1.0000 0.614 -0.0212 0.7167 0.239 0.390 0.4467 0.2244 0.3136
var3 0.775 0.6141 1.000 -0.1006 0.4470 0.563 0.403 0.5982 0.4815 0.2651
var4 -0.226 -0.0212 -0.101 1.0000 0.2136 0.331 0.189 -0.0544 0.0718 0.1688
var5 0.559 0.7167 0.447 0.2136 1.0000 0.249 0.483 0.3976 0.2189 -0.0407
var6 0.375 0.2391 0.563 0.3311 0.2486 1.000 0.419 0.1989 0.5319 0.3893
var7 0.429 0.3897 0.403 0.1888 0.4827 0.419 1.000 0.1419 0.4076 0.2742
var8 0.445 0.4467 0.598 -0.0544 0.3976 0.199 0.142 1.0000 0.5689 0.4473
var9 0.247 0.2244 0.481 0.0718 0.2189 0.532 0.408 0.5689 1.0000 0.3638
var10 0.336 0.3136 0.265 0.1688 -0.0407 0.389 0.274 0.4473 0.3638 1.0000
あるいは，print.default(result) のようにすればすべての結果を出力することができる。
> print.default(result)
$rotation # 因子軸の回転法
[1] "Varimax"
$correlation.matrix # 相関係数行列
var1 var2 var3 var4 var5 var6 var7 var8
var1 1.0000000 0.84487442 0.7746348 -0.22572126 0.5585596 0.3746964 0.4288587 0.44474253
var2 0.8448744 1.00000000 0.6140948 -0.02116982 0.7166837 0.2391217 0.3897472 0.44666435
var3 0.7746348 0.61409482 1.0000000 -0.10056276 0.4470492 0.5628616 0.4030052 0.59819255
var4 -0.2257213 -0.02116982 -0.1005628 1.00000000 0.2136123 0.3311048 0.1888090 -0.05438703
var5 0.5585596 0.71668368 0.4470492 0.21361227 1.0000000 0.2485824 0.4826623 0.39756234
var6 0.3746964 0.23912166 0.5628616 0.33110479 0.2485824 1.0000000 0.4191012 0.19885885
var7 0.4288587 0.38974717 0.4030052 0.18880904 0.4826623 0.4191012 1.0000000 0.14187410
var8 0.4447425 0.44666435 0.5981926 -0.05438703 0.3975623 0.1988589 0.1418741 1.00000000
var9 0.2466372 0.22442056 0.4814589 0.07176501 0.2189180 0.5319358 0.4075537 0.56891499
var10 0.3362334 0.31363051 0.2651037 0.16878738 -0.0407357 0.3893330 0.2741899 0.44734094
var9 var10
var1 0.24663719 0.3362334
var2 0.22442056 0.3136305
var3 0.48145888 0.2651037
var4 0.07176501 0.1687874
var5 0.21891798 -0.0407357
var6 0.53193583 0.3893330
var7 0.40755369 0.2741899
var8 0.56891499 0.4473409
var9 1.00000000 0.3637659
var10 0.36376593 1.0000000
$communality # 共通性
var1 var2 var3 var4 var5 var6 var7 var8 var9 var10
0.8782869 0.8058379 0.7376875 0.5392022 0.7962812 0.5710556 0.3852000 0.4574828 0.5682011 0.3258559
$before.rotation.fl # 回転前の因子負荷量
FAC.1 FAC.2 FAC.3
var1 -0.85127134 -0.38093708 -0.09225476
var2 -0.80339537 -0.36668776 0.16104011
var3 -0.83136537 -0.04526261 -0.21088020
var4 -0.06449186 0.52620168 0.50808939
var5 -0.67637810 -0.22526754 0.53670139
var6 -0.57352146 0.49150559 0.02347232
var7 -0.55425633 0.17470446 0.21789501
var8 -0.61545313 0.03446450 -0.27841064
var9 -0.56939070 0.42882823 -0.24515650
var10 -0.42989384 0.30434024 -0.22005500
$before.rotation.eval # 回転前の固有値
FAC.1 FAC.2 FAC.3
4.0468459 1.1590592 0.8591861
$after.rotation.fl # 回転後の因子負荷量
FAC.1 FAC.2 FAC.3
var1 -0.81752240 0.38107025 -0.25441993
var2 -0.86716928 0.22560900 -0.05436886
var3 -0.58096539 0.61850727 -0.13272345
var4 0.04083323 0.06991167 0.72982686
var5 -0.83442587 0.02649545 0.31513908
var6 -0.18699075 0.63098561 0.37141241
var7 -0.41170256 0.33927289 0.31716695
var8 -0.34888652 0.56003956 -0.14871696
var9 -0.11753949 0.73398757 0.12509133
var10 -0.08607321 0.56160143 0.05523714
$after.rotation.eval # 回転後の因子負荷量の二乗和
FAC.1 FAC.2 FAC.3
2.8031906 2.2652820 0.9966186
$scores # 因子得点
FAC.1 FAC.2 FAC.3
1 -2.35863255 0.63067260 0.329220617
2 -1.27981713 0.58243865 1.174903000
3 -0.06492078 1.18107012 0.889716371
4 -0.77918746 0.87233382 -1.166728853
5 -0.34036193 0.73957325 0.183002359
6 0.74062447 1.37316866 0.447702634
7 -0.46817258 -0.47855965 1.607620790
8 -0.30749799 -0.17331089 0.370604867
9 -0.83009214 0.44493091 -1.941757717
10 0.41762185 0.65611503 -0.170693247
11 0.79272411 0.15871956 -0.164168839
12 0.22027197 -0.14173994 -0.006421007
13 -1.08753778 -1.29541749 -0.451412084
14 1.16049740 0.05318377 0.933139700
15 1.31738669 -0.05099253 -0.583232459
16 1.33358487 0.69466121 -1.145936980
17 0.03587380 -0.72694479 -0.881790129
18 -0.43093588 -1.74621258 -0.621098893
19 1.07368915 -1.08529807 0.731121280
20 0.85488189 -1.68839164 0.466208591
attr(,"class")
[1] "pfa"
plot メソッド
> plot(result, axis=FALSE, pch=19, main="因子負荷量") # 因子負荷量のプロット
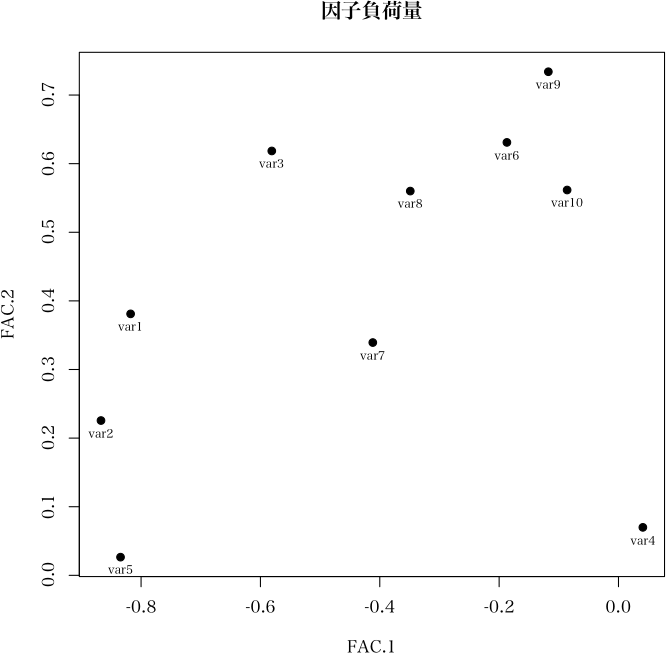> plot(a, pch=19, scores=TRUE) # 因子得点のプロット
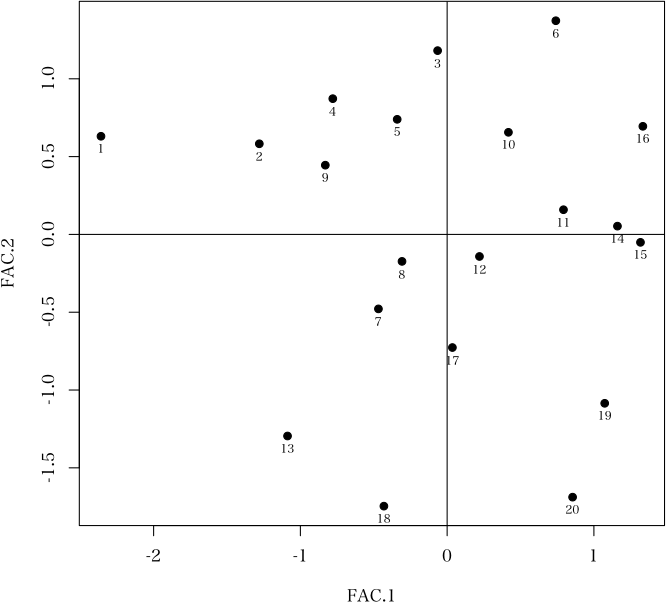
解説ページ
直前のページへ戻る E-mail to Shigenobu AOKI
