Deming 法による回帰直線のパラメータ Last modified: Sep 03, 2009
目的
Deming 法による回帰直線のパラメータを求める。
使用法
Deming(x, y, n=1, a=1)
# print メソッド
print.deming(obj, digits=5, sig=0.95)
# plot メソッド
plot.deming(obj, posx="topleft", posy=NULL, xlab=obj$names.xy[1], ylab=obj$names.xy[2], hist=FALSE, ...)
引数
x 独立変数ベクトル
y 従属変数ベクトル
n ブートストラップ法で信頼区間を求めるときの回数
デフォルトは 1。この場合には信頼区間を求めない
a 分散比
デフォルトは 1。
大きくすると普通の回帰直線に近づく。小さくすると本法の特徴が強く表れる。
obj "deming" オブジェクト
digits 表示桁数
sig ブートストラップ法による信頼限界を求めるときの信頼度(デフォルトで 95% 信頼限界)
posx, posy legend 関数のための位置引数("topleft", "bottomright" なども可)
xlab, ylab 軸の名前
hist ブートストラップ法による結果のヒストグラム表示をするかどうか
... plot 関数に渡されるその他の引数
ソース
インストールは,以下の 1 行をコピーし,R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/Deming.R", encoding="euc-jp")
# Deming 法による回帰直線のパラメータ推定
Deming <- function( x, # 独立変数ベクトル
y, # 従属変数ベクトル
n=1, # ブートストラップ法で信頼区間を求めるときの回数
a=1) # 分散比
{
Deming0 <- function(x, y) # 1 組のデータについて,切片と傾きの推定値を計算する
{
sxx <- sum((x-mean(x))^2)
syy <- sum((y-mean(y))^2)
sxy <- sum((x-mean(x))*(y-mean(y)))
if (sxy != 0) {
Slope <- (syy-a*sxx+sqrt((syy-a*sxx)^2+4*a*sxy^2))/(2*sxy)
Intercept <- mean(y)-Slope*mean(x)
} else {
Slope <- Intercept <- NA
}
return(c(Intercept=Intercept, Slope=Slope))
}
Driver <- function(x, y) # ブートストラップ法のためのドライバー
{
n <- length(x)
suffix <- sample(n, n, replace=TRUE) # リサンプリング
return(Deming0(x[suffix], y[suffix])) # リサンプリングしたデータについてパラメータを推定
}
names.xy <- c(deparse(substitute(x)), deparse(substitute(y))) # 変数名を控えておく
OK <- complete.cases(x, y) # 欠損値を持つケースを除く
x <- x[OK]
y <- y[OK]
ans <- list(coefficients=Deming0(x, y), # 引数に対してパラメータを推定する
names.xy=names.xy, x=x, y=y)
if (n > 1) {
ans2 <- replicate(n, Driver(x, y)) # ブートストラップを n 回実行
ans <- append(ans, list(intercepts=ans2[1,], slopes=ans2[2,]))
}
class(ans) <- "deming" # print, plot メソッドのためにクラス名をつけておく
return(ans)
}
# print メソッド
print.deming <- function( obj, # "deming" オブジェクト
digits=5, # 表示桁数
sig=0.95) # 信頼度
{
if (length(obj) == 4) {
cat("Intercept:", round(obj$coefficients[1], digits),
" Slope:", round(obj$coefficients[2], digits), "\n")
}
else {
alpha <- (1-sig)/2
LCL <- c(quantile(obj$intercepts, alpha, na.rm=TRUE), quantile(obj$slopes, alpha, na.rm=TRUE))
UCL <- c(quantile(obj$intercepts, 1-alpha, na.rm=TRUE), quantile(obj$slopes, 1-alpha, na.rm=TRUE))
ans <- data.frame(obj$coefficients, LCL, UCL)
dimnames(ans) <- list(c("Intercept:", "Slope:"),
c("Estimate", paste(c(alpha, 1-alpha), "%", sep="")))
print(round(ans, digits=digits))
}
}
# plot メソッド
plot.deming <- function(obj, # "deming" オブジェクト
posx="topleft", posy=NULL, # legend 関数のための位置引数
xlab=obj$names.xy[1], ylab=obj$names.xy[2], # 軸の名前
hist=FALSE, # ヒストグラムを描くとき TRUE にする
...) # その他の任意の plot 関数の引数
{
if (hist && length(obj) == 6) { # ブートストラップの結果を,hist=TRUE のときに,ヒストグラムで表示する
layout(matrix(1:2, 2))
hist(obj$intercepts, xlab="Intercept", main="", right=FALSE)
hist(obj$slopes, xlab="Slope", main="", right=FALSE)
layout(1)
}
else { # 散布図と Deming 法の回帰直線と直線回帰式を表示する
plot(obj$x, obj$y, xlab=xlab, ylab=ylab, ...)
abline(obj$coefficients)
abline(lm(obj$y~obj$x), lty=2, col=2)
legend(posx, posy, legend=c("Deming", "linear regression"), lty=1:2, col=1:2)
}
}
使用例
> set.seed(123)
> d <- gendat2(100, 0.7)*15+50
> (a <- Deming(d[,1], d[,2])) # 点推定値のみを求める
Intercept: 0 Slope: 1
> plot(a, xlab="x", ylab="y", pch=19, xlim=c(0,100),ylim=c(0,100)) # 散布図と回帰直線
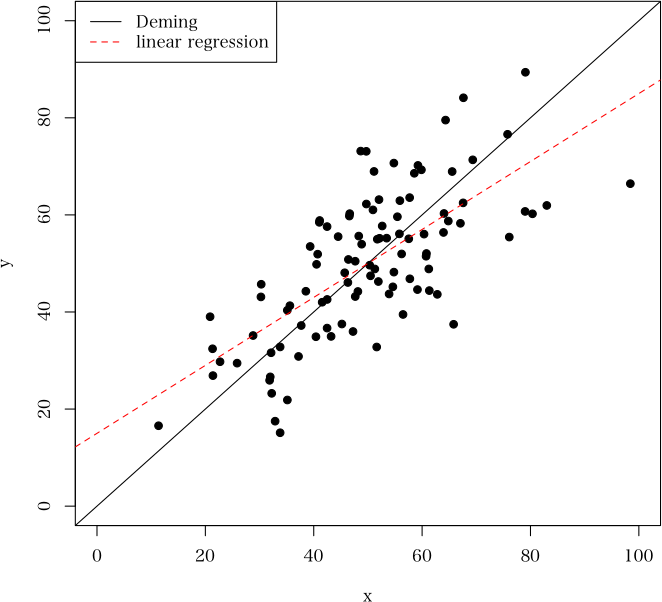 > (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
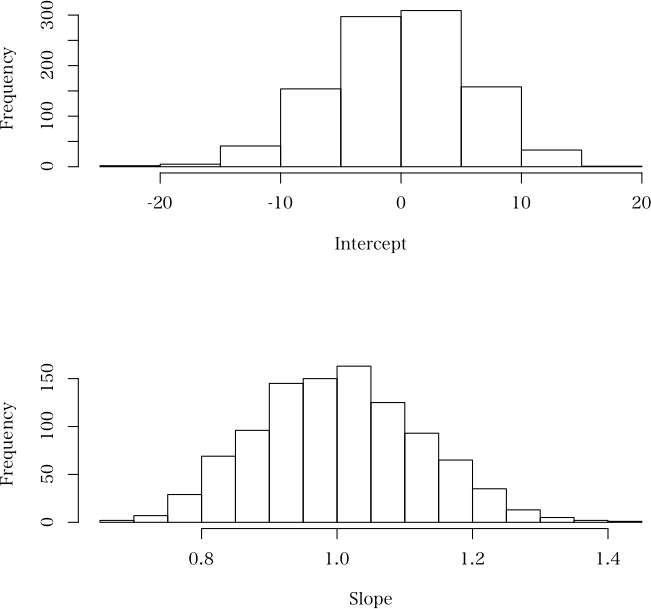
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図
> (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図
 直前のページへ戻る
直前のページへ戻る  E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI

 > (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図
> (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図

 > (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図
> (b <- Deming(d[,1], d[,2], n=1000)) # 点推定値と信頼区間を求める
Estimate 0.025% 0.975%
Intercept: 0 -11.66837 10.4718
Slope: 1 0.78298 1.2427
> plot(b, hist=TRUE) # ブートストラップパラメータの分布図
