目的

Box-Cox 変換の，最適のλを図により求める

使用法

Box.Cox.transformation(x, l=-3, r=3, delta=0.1)

引数

x       データベクトル
l, r    λの探索範囲
delta   探索ステップ

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/Box_Cox_transformation.R", encoding="euc-jp")

# Box-Cox 変換の，最適のλを図により求める
Box.Cox.transformation <- function(  x,                      # データ
                                        l=-3, r=3,              # λの探索範囲
                                        delta=0.1)              # 探索ステップ
{
        x <- x[!is.na(x)]                                    # 有効データのみを対象とする
        Gm <- exp(mean(log(x)))                                      # 幾何平均を求める
        lambda0 <- seq(l, r, delta)                          # 候補とするλの値のベクトル
        result <- numeric(length(lambda0))                   # 変換値を保存するベクトル
        for (i in seq(along=lambda0)) {                         # λの各候補ごとに，
                lambda <- lambda0[i]
                if (lambda == 0) {
                        w <- Gm*log(x)
                }
                else {
                        w <- (x^lambda-1)/(lambda*Gm^(lambda-1))
                }
                result[i] <- sd(w)                           # 変換結果を保管
        }
        plot(lambda0, result, type="l")                         # 図に描く
}


使用例

> x <- c(5.0, 5.0, 3.3, 4.3, 4.0, 5.5, 4.0, 6.0, 5.0, 5.0, 4.0, 4.3, 5.3, 5.0, 6.0, 6.7, 6.5, 6.0, 6.0, 5.3, 7.0, 5.0, 6.3, 5.3, 4.5, 6.0, 7.0,
+ 2.0, 2.5, 1.5, 1.7, 1.0, 1.0, 2.0, 1.0, 1.7, 2.0, 2.0, 1.0, 1.3, 2.5, 1.0, 2.0, 2.0, 1.0, 3.0, 1.3, 1.0, 2.0, 2.0, 1.7, 1.0, 1.0, 1.0,
+ 4.0, 5.3, 3.0, 3.7, 2.7, 3.3, 5.0, 2.7, 4.7, 3.7, 3.7, 4.0, 4.7, 4.3, 5.7, 4.7, 5.3, 5.5, 4.3, 7.0, 5.0, 5.3, 5.7, 5.3, 4.3, 5.0, 5.0, 5.0, 4.3, 4.7,
+ 1.3, 1.3, 1.3, 1.7, 2.0, 1.0, 1.3, 1.3, 1.7, 1.7, 1.3, 1.3, 1.3, 2.3, 2.0, 2.7, 2.0, 1.7, 2.3, 1.0, 2.0, 2.0, 2.0, 1.7, 2.0, 1.3, 1.3, 2.0, 1.3, 1.7,
+ 5.0, 5.0, 3.7, 3.3, 3.0, 3.5, 3.3, 3.0, 3.0, 4.3, 3.7, 4.0, 4.0, 3.3, 5.0, 6.0, 4.0, 4.0, 5.7, 5.5, 5.5, 5.5, 5.3, 4.7, 5.0, 4.3, 4.3, 3.0, 6.0,
+ 2.3, 1.7, 2.0, 1.0, 1.5, 1.0, 1.0, 2.0, 1.0, 2.0, 1.3, 1.7, 1.7, 2.0, 2.0, 2.0, 1.7, 2.0, 1.7, 0.5, 1.7, 1.3, 1.7, 2.3, 2.0, 1.0, 1.0, 1.3, 2.0,
+ 2.0, 5.5, 3.5, 5.3, 5.0, 6.0, 8.0, 6.0, 4.0,
+ 2.0, 3.0, 2.5, 2.0, 1.0, 2.0, 1.0, 3.0, 2.0)

> Box.Cox.transformation(x)

以下のような図が描かれる



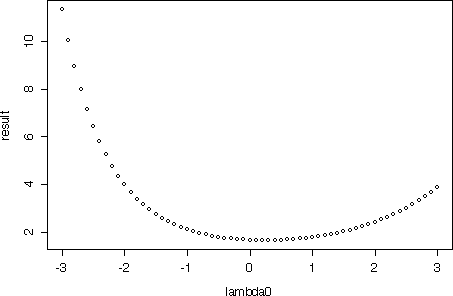
 注：得られたλをそのまま採用するのではなく，意味の明らかな近傍の値を採用するべきである。
　　　たとえば上の図では，λ = 0 すなわち，対数変換をするのが妥当であろう。
　　　λ = 0.5 は，平方根変換
　　　λ = -1 は逆数変換
　　　λ = 1 のときは，単なる線形変換（もとのデータから 1 引くだけ）なので，分布型は変わらない。