目的

AIC により，最適な度数分布表となる階級分けを探索する。

使用法

AIC.Histogram(x, d = 0, c = floor(2*sqrt(length(x))-1))

引数

x データベクトル
d 測定精度（無限の精度の場合には 0
c 初期階級数

ソース

インストールは，以下の 1 行をコピーし，R コンソールにペーストする
source("http://aoki2.si.gunma-u.ac.jp/R/src/AIC-Histogram.R", encoding="euc-jp")

# AIC による，ヒストグラム（度数分布表）の最適階級分割の探索
#
AIC.Histogram <- function(   x,                                      # データベクトル
                                d = 0,                                  # 測定精度（無限の精度の場合には 0
                                c = floor(2*sqrt(length(x))-1)) {       # 初期階級数
        MODEL <- function(c1, r, c2, n, c)                           # 個別の度数分布表の AIC の計算
        {
                logNZ <- function(x, y) {                            # 補助関数
                        return(ifelse(x > 0, x*log(x/y) , 0))
                }
                N <- sum(n)                                          # サンプルサイズ
                sum1 <- sum(n[1:c1])                                 # 左端で併合され階級について
                sum2 <- sum(n[(c-c2+1):c])                           # 右端で併合され階級について
                cc1c2r1 <- (c-c1-c2)/r+1                             # 中央部分で併合され階級について
                temp <- 0
                for (j in 2:cc1c2r1) {
                        sum3 <- sum(n[(c1+(j-2)*r+1):(c1+(j-1)*r)])
                        temp <- temp+logNZ(sum3, r*N)
                }
                AIC <- -2*(logNZ(sum1, c1*N)+temp+logNZ(sum2, c2*N))+2*cc1c2r1 # モデルの AIC
                return(AIC)
        }
        x <- x[!is.na(x)]                                            # 完全なデータについて
        N <- length(x)                                                       # サンプルサイズ
        brks = seq(min(x)-d/2, max(x)+d/2, length=c+1)                  # 分割点
        ans <- hist(x, breaks=brks, plot=FALSE, right=FALSE)         # 度数分布表を得る
        n <- ans$count                                                       # 度数ベクトル
        result <- NULL                                                       # 結果の蓄積用
        for (c1 in 1:(c-2)) {                                           # 左端で併合する階級数を探索
                for (c2 in 1:(c-2)) {                                   # 右端で併合する階級数を探索
                        if (c <= c1+c2) next                         # 制約条件を満たさない場合は次へ
                        for (r in 1:(c-c1-c2)) {                        # 中央付近で併合する階級数を探索
                                if ((c-c1-c2)%%r == 0) {                # 併合する階級数は等しくする必要がある
                                        result <- append(result, list(c1, r, c2, MODEL(c1, r, c2, n, c)))
                                }
                        }
                }
        }
        p <- n/N*100                                                 # パーセント
        df <- data.frame(matrix(unlist(result), ncol=4, byrow=TRUE)) # 結果をデータフレームに変換
        colnames(df) <- c("c1", "r", "c2", "AIC")                    # 列に名前を付ける
        o <- order(df[,4])                                           # AIC の小さい順
        df <- df[o,]                                                 # 並べ替える
        plot(range(brks), c(0, max(p)), type="n", xlab="data", ylab="Percent")          # プロット枠組み
        sapply(1:(N-1), function(i) rect(brks[i], 0, brks[i+1], p[i], border="gray"))   # 初期ヒストグラム
        c1 <- df[1,1]                                                        # 最適モデルの結果取り出し
        r <- df[1,2]
        c2 <- df[1,3]
        AIC <- df[1,4]
        lo <- brks[1]                                                        # 階級の開始値
        delta <- diff(brks[1:2])                                     # 階級幅
        m <- (c-c1-c2)/r                                             # 中央付近の併合後階級数
        cmg <- cumsum(c(0, c1, rep(r, m), c2))                               # 併合後の階級の開始値ベクトル
        sapply(1:(m+2), function(i) rect(lo+cmg[i]*delta, 0,            # 併合後のヒストグラム
                lo+cmg[i+1]*delta, mean(p[(cmg[i]+1):(cmg[i+1])]),
                border="red", col="red", density=15))
        mtext(paste("AIC =", round(AIC, 2)), side=3, line=-1.2,         # AIC を図に書き込む
                at=lo+0.8*c*delta)
        invisible(list(df=df, n=n, breaks=brks))                        # 結果を返す
}


使用例

x <- c(28.67, 40.29, 10.61, 33.85, 36.19, 20.63, 9.64, 15.26,
  15.53, 73.62, 63.29, 32.77, 32.28, 11.90, 54.16, 4.73, 24.67,
  17.66, 25.84, 22.89, 15.68, 5.48, 36.41, 20.33, 44.58, 57.23,
  65.89, 57.91, 2.39, 9.15, 10.27, 3.04, 12.35, 32.78, 44.23,
  31.14, 6.03, 27.90, 28.73, 42.09, 3.99, 9.74, 6.85, 0.16, 9.26,
  7.72, 34.42, 32.77, 6.80, 10.45, 29.80, 5.89, 13.56, 50.55, 0.51,
  0.19, 7.19, 5.94, 11.24, 32.32, 15.27, 29.64, 10.03, 2.01, 13.89,
  20.83, 27.49, 14.46, 8.22, 27.81, 33.65, 38.57, 8.66, 1.40,
  23.97, 15.11, 63.32, 7.76, 1.58, 48.66, 44.46, 0.02, 38.12,
  18.51, 101.75, 34.16, 27.99, 5.22, 1.82, 8.22, 4.89, 97.50, 2.10,
  26.19, 10.11, 8.39, 25.83, 1.05, 25.63, 18.35)
ans <- AIC.Histogram(x, 0.01)
str(ans)
ans$df[1:10,]

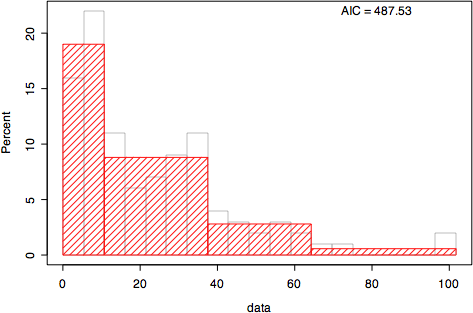
出力結果例

> x <- c(28.67, 40.29, 10.61, 33.85, 36.19, 20.63, 9.64, 15.26,
+   15.53, 73.62, 63.29, 32.77, 32.28, 11.90, 54.16, 4.73, 24.67,
+   17.66, 25.84, 22.89, 15.68, 5.48, 36.41, 20.33, 44.58, 57.23,
+   65.89, 57.91, 2.39, 9.15, 10.27, 3.04, 12.35, 32.78, 44.23,
+   31.14, 6.03, 27.90, 28.73, 42.09, 3.99, 9.74, 6.85, 0.16, 9.26,
+   7.72, 34.42, 32.77, 6.80, 10.45, 29.80, 5.89, 13.56, 50.55, 0.51,
+   0.19, 7.19, 5.94, 11.24, 32.32, 15.27, 29.64, 10.03, 2.01, 13.89,
+   20.83, 27.49, 14.46, 8.22, 27.81, 33.65, 38.57, 8.66, 1.40,
+   23.97, 15.11, 63.32, 7.76, 1.58, 48.66, 44.46, 0.02, 38.12,
+   18.51, 101.75, 34.16, 27.99, 5.22, 1.82, 8.22, 4.89, 97.50, 2.10,
+   26.19, 10.11, 8.39, 25.83, 1.05, 25.63, 18.35)
> ans <- AIC.Histogram(x, 0.01)
> str(ans)
List of 3
 $ df    :'data.frame':	416 obs. of  4 variables:
  ..$ c1 : num [1:416] 2 2 3 2 3 2 3 3 2 3 ...
  ..$ r  : num [1:416] 5 5 5 6 4 3 5 4 4 2 ...
  ..$ c2 : num [1:416] 7 2 1 5 8 2 6 4 1 8 ...
  ..$ AIC: num [1:416] 488 489 490 491 491 ...
 $ n     : int [1:19] 16 22 11 6 7 9 11 4 3 2 ...
 $ breaks: num [1:20]  0.015  5.370 10.724 16.079 21.434 ...
> ans$df[1:10,]
    c1 r c2      AIC
78   2 5  7 487.5261
60   2 5  2 488.7143
105  3 5  1 490.2904
72   2 6  5 490.6599
130  3 4  8 491.1111
59   2 3  2 491.6356
123  3 5  6 492.0030
116  3 4  4 492.4315
55   2 4  1 492.9979
129  3 2  8 493.2800



 参考文献
　　坂本慶行，石黒真木夫，北川源四郎「情報量統計学」共立出版株式会社