問：非線形最小二乗法を行いたいのですが，Excel でもできる簡単な方法はありますか？

R でもできる（R って？）。

Excel のソルバーを使うことで，非線形最小二乗法により実験値（測定値）に非線形関数をあてはめることができる。

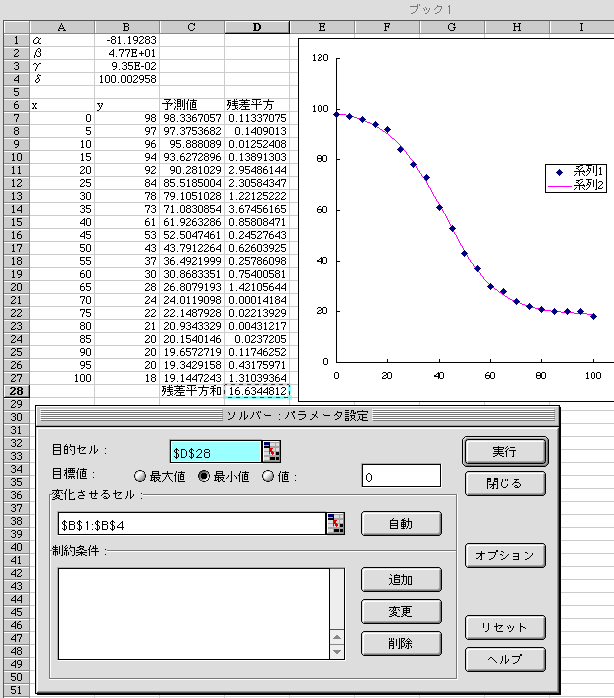
例： 表 1 のような x，y の測定値に対して，y = α / { 1 + β exp(-γx) } + δ という関数をあてはめ，パラメータ，α，β，γ，δを求める。

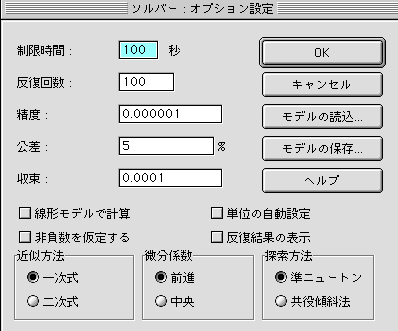
手順： 以下の通り

  1. 予測値を求める計算式を書き込む（C7:C27，表 2 参照）
    注：表 2 において，計算式中に含まれる α，β，γ，δ は，Excel の「セルに名前を付ける」という機能により，B1，B2，B3，B4 に付けた名前である（A 列にも α，β，γ，δ と書いてあるが，これを書いただけでは，セルに名前を付けたことにはならない）。名前を定義した後，名前を使って計算式を書く。名前を使わないでも計算式は書けるが，$B$1 などとしなくてはならず，面倒で，わかりにくい。
  2. 残差平方を求める式を書き込む（D7:D27，表 2 参照）
  3. 残差平方の和を求める式を書き込む（D28，表 2 参照）
  4. 求めるパラメータのセルに初期値を書き込んでおく（適当に）
    注：測定値と予測値を折れ線グラフなどで描くようにしておき，パラメータの候補値を幾組か入れて，予測値の変化を見ながら，絞っていくとよいかもしれない。
  5. 「ツール」メニューから「ソルバー...」を選ぶ（図1参照）
  6. 「目的セル:」の欄に，残差平方和の式を書き込んだセルを指定する（D28）
  7. 「目標値:」のラジオボタンは，「最小値」をチェックする
  8. 「オプション」ボタンをクリックしてオプションを設定する（図2参照）
    注：設定項目の詳細については，「ヘルプ」を参照のこと。
  9. 「実行」ボタンをクリックする

初期値が不適切な場合には，変更してから再度 5 以降を繰り返す。

・ 例題の Excel ファイルのダウンロード

表 1．使用例
A B C D
1 α -81.19283

2 β 4.77E+01

3 γ 9.35E-02

4 δ 100.0029575

5



6 x y 予測値 残差平方
7 0 98 98.33670573 0.11337075
8 5 97 97.37536822 0.140901299
9 10 96 95.88808895 0.012524082
10 15 94 93.62728961 0.138913032
11 20 92 90.28102896 2.954861435
12 25 84 85.5185004 2.305843466
13 30 78 79.10510281 1.221252223
14 35 73 71.08308538 3.674561651
15 40 61 61.92632862 0.85808471
16 45 53 52.50474609 0.245276431
17 50 43 43.79122642 0.626039253
18 55 37 36.49219986 0.25786098
19 60 30 30.86833508 0.754005812
20 65 28 26.80791928 1.421056443
21 70 24 24.01190982 0.000141844
22 75 22 22.14879279 0.022139295
23 80 21 20.9343329 0.004312169
24 85 20 20.1540146 0.023720497
25 90 20 19.65727194 0.117462522
26 95 20 19.34291575 0.431759712
27 100 18 19.14472426 1.310393638
28

残差平方和 16.63448124

表 2．各セルの数式
A B C D
1 α -81.1928300023457

2 β 47.7278281790319

3 γ 0.0935304121023703

4 δ 100.002957503194

5



6 x y 予測値 残差平方
7 0 98 =α/(1+β*EXP(-γ*A7))+δ =(B7-C7)^2
8 5 97 =α/(1+β*EXP(-γ*A8))+δ =(B8-C8)^2
9 10 96 =α/(1+β*EXP(-γ*A9))+δ =(B9-C9)^2
10 15 94 =α/(1+β*EXP(-γ*A10))+δ =(B10-C10)^2
11 20 92 =α/(1+β*EXP(-γ*A11))+δ =(B11-C11)^2
12 25 84 =α/(1+β*EXP(-γ*A12))+δ =(B12-C12)^2
13 30 78 =α/(1+β*EXP(-γ*A13))+δ =(B13-C13)^2
14 35 73 =α/(1+β*EXP(-γ*A14))+δ =(B14-C14)^2
15 40 61 =α/(1+β*EXP(-γ*A15))+δ =(B15-C15)^2
16 45 53 =α/(1+β*EXP(-γ*A16))+δ =(B16-C16)^2
17 50 43 =α/(1+β*EXP(-γ*A17))+δ =(B17-C17)^2
18 55 37 =α/(1+β*EXP(-γ*A18))+δ =(B18-C18)^2
19 60 30 =α/(1+β*EXP(-γ*A19))+δ =(B19-C19)^2
20 65 28 =α/(1+β*EXP(-γ*A20))+δ =(B20-C20)^2
21 70 24 =α/(1+β*EXP(-γ*A21))+δ =(B21-C21)^2
22 75 22 =α/(1+β*EXP(-γ*A22))+δ =(B22-C22)^2
23 80 21 =α/(1+β*EXP(-γ*A23))+δ =(B23-C23)^2
24 85 20 =α/(1+β*EXP(-γ*A24))+δ =(B24-C24)^2
25 90 20 =α/(1+β*EXP(-γ*A25))+δ =(B25-C25)^2
26 95 20 =α/(1+β*EXP(-γ*A26))+δ =(B26-C26)^2
27 100 18 =α/(1+β*EXP(-γ*A27))+δ =(B27-C27)^2
28

残差平方和 =SUM(D7:D27)

図 1．ソルバーのダイアログボックス
fig1

図 2．ソルバーのオプション
fig2

Last modified: Jul 16, 2004

・ 直前のページへ戻る　　・ E-mail to Shigenobu AOKI